Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì BI và CI là phân giác => AI cũng là phân giác
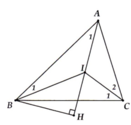
Ta có \(\widehat{\text{BAI}}=\widehat{CAH}=\frac{\widehat{BAC}}{2}\) ( AI là phân giác)
\(\widehat{\text{ACI}}\)=\(\widehat{\text{BCI}}\)=\(\frac{\widehat{\text{ACB}}}{2}\)(CI là phân giác)
\(\widehat{\text{ABI}}=\)\(\widehat{\text{CBI}}=\)\(\widehat{\frac{\text{ABC}}{2}}\) (BI là phân giác)
Xét tam giác vuông \(AHB\Rightarrow\widehat{IAB}+\widehat{ABH}=90^0\)\(\text{AHB => IAB + ABH = 90}\)
\(\Rightarrow IAB+ABI+IBH=90^0\)
\(\Rightarrow IBH=90^0-\left(IAB+ABI\right)\left(1\right)\)
Xét \(\Delta ABC\) có \(\widehat{\text{BAC}}\)\(+\widehat{\text{ABC}}\)\(+\widehat{\text{ACB}}\)\(\text{= 180}^0\)
\(\Rightarrow\frac{\left(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}\right)}{2}=\frac{180^0}{2}=90^0\)
\(\frac{\widehat{BAC}}{2}+\widehat{\frac{ABC}{2}}+\frac{\widehat{ACB}}{2}=90^0\)
Lại có \(\widehat{\text{BAI}}\) \(=\widehat{\text{CAH}}\) \(=\frac{\widehat{BAC}}{2}\) \(;\widehat{\text{ABI}}\)\(=\widehat{\text{CBI}}=\)\(\frac{\widehat{\text{ABC}}}{2}\) và \(\widehat{\text{ABI}}=\)\(\widehat{\text{CBI}}\)\(=\widehat{\frac{\text{ABC}}{2}}\)
\(\Rightarrow\) \(\widehat{\text{IAB}}\) +\(\widehat{\text{ ABI}}\) + \(\widehat{\text{ACI}}=90^0\)
\(\Rightarrow\widehat{\text{ACI }}=90^0-\left(\widehat{IAB}+\widehat{ABH}\right)\left(2\right)\)
Từ (1) và (2) => \(\widehat{\text{IBH}}=\widehat{ACI}\)





Mỗi học sinh được thưởng số quyển vở là:
56 : 7 = 8 (quyển)
Số quyển vở để thưởng cho 23 bạn học sinh giỏi là:
8 * 23 = 184 (quyển)
Đáp số : 184 quyển vở