Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

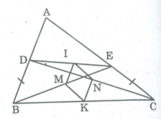
*Trong ∆ BCD,ta có:
K là trung điểm của BC (gt)
N là trung điểm của CD (gt)
Nên NK là đường trung bình của ∆ BCD
⇒ NK // BD và NK = 1/2 BD (1)
*Trong ∆ BED,ta có:
M là trung điểm của BE (gt)
I là trung điểm của DE (gt)
Nên MI là đường trung bình của ∆ BED
⇒ MI // BD và MI = 1/2 BD (t/chất đường trung bình trong tam giác) (2)
Từ (1) và (2) suy ra: MI // NK và MI = NK
Nên tứ giác MKNI là hình bình hành.
*Trong ∆ BEC ta có MK là đường trung bình.
⇒ MK = 1/2 CE (t/chất đường trung bình của tam giác)
BD = CE (gt). Suy ra: MK = KN
Vậy hình bình hành MKNI là hình thoi.
⇒IK ⊥ MN (t/chất hình thoi).

a: Xét ΔBEC có
I là trung điểm của BE
M là trung điểm của BC
Do đó: IM là đường trung bình của ΔBEC
Suy ra: \(IM=\dfrac{EC}{2}\left(1\right)\)
Xét ΔDCB có
K là trung điểm của DC
M là trung điểm của BC
Do đó: KM là đường trung bình của ΔDCB
Suy ra: \(KM=\dfrac{BD}{2}\)
mà BD=CE
nên \(KM=\dfrac{CE}{2}\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra IM=KM


Áp dụng định lí về đường trung bình của tam giác để chứng minh MI = IN = NK = KM (cùng bằng \(\dfrac{BD}{2}\) và \(\dfrac{CE}{2}\) )
MINK là hình thoi nên \(IK\perp MN\)