Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Bán kính đường tròn ngoại tiếp tam giác là R = B C 2 sin A = 3 2 sin 60 = 3
Độ dài đường cao là A H = A B sin B 3 3 2
Khi quay quanh đường thẳng AD
Thể tích hình cầu tạo thành là V 1 = 4 3 π R 3 = 4 π 3
Thể tích khối nón tạo thành là V 1 = 1 3 π r 2 h = 1 3 π H B 2 . A H = 23 8 π 3

Đáp án B
Bán kính đường tròn ngoại tiếp tam giác là: R = B C 2 sin A = 30 2 sin 60 = 3
Độ dài đường cao là A H = A B sin B = 3 3 2
Khi quay quanh đường thẳng AD
Thể tích hình cầu tạo thành là: V 1 = 4 3 π R 3 = 4 π 3
Thể tích khối nón tạo thành là: V 2 = 1 3 π r 2 h = 1 3 π H B 2 . A H = 23 8 π 3

Đáp án C
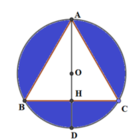
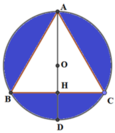
Phương pháp: Thể tích của khối tròn xoay sinh khi cho phần tô đậm (hình vẽ) quay quanh đường thẳng AD bằng thể tích hình cầu đường kính AD trừ đi thể tích hình nón tạo bởi khi quay tam giác ABC quanh trục AD.
Cách giải:
*) Tính thể tích hình cầu đường kính AD:
Tam giác ABC đều, cạnh a
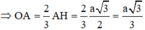
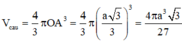
*) Tính thể tích hình nón (H) tạo bởi khi quay tam giác ABC quanh trục AH:
Hình nón (H) có đường cao 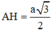 , bán kính đáy
, bán kính đáy 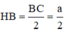
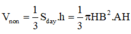
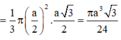
*) Tính V
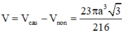

Thể tích cần tìm bằng thể tích của khối cầu đường kính AD trừ đi thể tích khối nón sinh bởi tam giác ABC khi quay quanh trục AD.
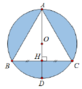
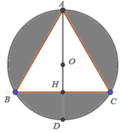
+) ∆ A D C vuông tại C ⇒ a D = A C c o s D A C = a 3 2 = 2 a 3
⇒ Bán kính khối cầu đường kính AD là: R = a 3
⇒ V c a u = 4 3 π . a 3 3 = 4 πa 3 3 27
+) ∆ A B C đều cạnh a ⇒ A H = a 3 3 r = H B = H C = a 2
Thể tích khối nón là:
V n o n = 1 3 π ( a 2 ) 2 . a 3 2 = πa 3 3 24
Thể tích cần tìm là:
V = 4 πa 3 3 27 - πa 3 3 24 = 24 πa 3 3 216
Chọn đáp án D.

Đáp án A
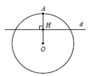
Khi quay hình tròn C quay trục OA ta được khối cầu có thể tích V = 4 3 π R 3 = 36 π
Khối tròn xoay H 1 chưa điểm A chính là chỏm cầu có chiều cao x 2 + 4
Suy ra thể tích khối H 1 là V 1 = π h 2 R − h 3 = π . A H 2 . 3 − A H 3
Mà V = V 1 + V 2 và
V 2 = 2 V 1 ⇒ V 1 V = 1 3 = A H 2 . 3 − A H 3 36 = 1 3 ⇔ A H 3 − 9 A H 2 + 36 = 0 *
Vì 0 < A H < O A = 3 nên giải * → c a s i o A H ≈ 2 , 32

Đáp án A
Khi quay quanh AB, hình vuông ABCD sinh ra mặt trụ có thể tích V 1 = πa 3
Hình thang AMCB sinh ra hình nón cụt có thể tích
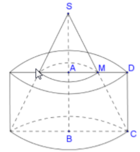

Đáp án D
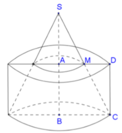
Khi quay quanh AB, hình vuông ABCD sinh ra mặt trụ có thể tích V 1 = πa 3
Hình thang AMCB sinh ra hình nón cụt có thể tích
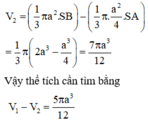

Đáp án A.
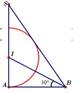
Đặt SA = h tam giác SAB vuông tại A ⇒ A B = S A tan 60 ° = h 3 .
Tam giác IAB vuông tại A ⇒ tan I B A ^ = I A A B ⇒ I A = h 3 .
Khi quay tam giác SAB quay trục SA, ta được khối nón có chiều cao h, bán kính r = h 3 ,
Và quay nửa đường tròn quanh trục SA, ta được khối cầu có bán kính R = h 3 .
Vậy V 1 = 1 3 πr 2 h = 1 3 π . h 3 2 h = πh 3 9 V 2 = 4 3 πR 2 = 4 3 π h 3 3 = 4 πh 3 81 ⇒ V 1 V 2 = 1 9 : 4 81 = 9 4 ⇒ 4 V 1 = 9 V 2 .
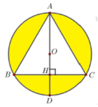

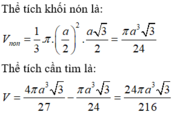
Đáp án đúng : A