Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Có cần chứng minh không ?
Mình chỉ biết 2 điểm thẳng hàng là B, K, N và C, K, P.
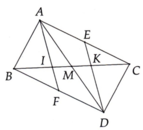
b) Xét tam giác AKC có:
KN là trung tuyến
CI là trung tuyến
CI cắt KN tại D
=> D là trọng tâm của tam giác AKC (đpcm) (1)
c) Từ (1) => \(DK=\frac{2}{3}KN\)
Mà \(D\in KN\)=> \(DK+DN=KN\)
Ngoặc ''}'' 2 điều
\(\Rightarrow\frac{2}{3}KN+DN=KN\)
\(\Rightarrow DN=KN-\frac{2}{3}KN=\frac{1}{3}KN\)
Xét tam giác ABC có:
AM là trung tuyến
BN là trung tuyến
AM cắt BN tại K
=> K là trọng tâm của tam giác ABC (2)
Từ (2) => \(KB=\frac{2}{3}BN\)
Mà \(K\in BN\)=> \(KB+KN=BN\)
Ngoặc ''}'' 2 điều
\(\Rightarrow\frac{2}{3}BN+KN=BN\)
\(\Rightarrow KN=BN-\frac{2}{3}BN=\frac{1}{3}BN\)
Mà \(DN=\frac{1}{3}KN\)(cmt)
\(\Rightarrow DN=\frac{1}{3}.\frac{1}{3}BN=\frac{1}{9}BN\)
Mà BN = 18cm (GT)
\(\Rightarrow DN=\frac{1}{9}.18=2cm\)(đpcm)

Bạn tự vẽ hình nha![]()
a.
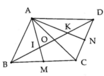
Xét tam giác ABO và tam giác CDO có:
AO = CO (BO là trung truyến của tam giác ABC)
AOB = COD (2 góc đối đỉnh)
BO = DO (gt)
=> Tam giác ABO = Tam giác CDO (c.g.c)
=> BAO = DCO (2 góc tương ứng)
mà 2 góc này ở vị trí so le trong
=> AB // CD.
b.
BO là trung tuyến của tam giác ABC
=> O là trung điểm của AC
=> AO = CO = \(\frac{1}{2}AC\) (1)
- BO = DO (gt) => CO là trung tuyến của tam giác BCD
- BM = CM (M là trung điểm của BC) => DM là trung tuyến của tam giác BCD
=> I là giao điểm của 2 đường trung tuyến CO và DM của tam giác BCD
=> I là trọng tâm của tam giác BCD.
=> IO = \(\frac{1}{3}OC\) (2)
Thay (1) vào (2), ta có:
IO = \(\frac{1}{3}OC=\frac{1}{3}\times\frac{1}{2}AC=\frac{1}{6}AC\)
\(\Rightarrow AC=6\times IO\)
c.
AB // CD
=> EBM = DCM (2 góc so le trong)
Xét tam giác EBM và tam giác DCM có:
EBM = DCM (chứng minh trên)
BM = CM (M là trung điểm của BC)
BME = CMD (2 góc đối đỉnh)
=> Tam giác EBM = Tam giác DCM (g.c.g)
=> BE = CD (2 cạnh tương ứng)
mà CD = AB (tam giác ABO = tam giác CDO)
=> BE = AB.
Chúc bạn học tốt![]()