Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

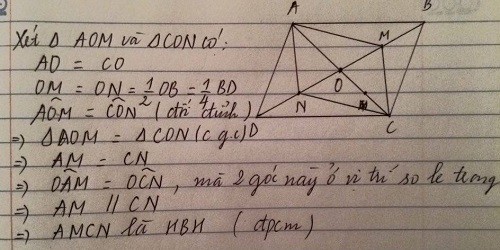
a: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành

a) Vì ABCD là hình thoi(gt). Mà AC và BD cắt nhau tại O
=> O là trung điểm của AC và BD (t/c của hình bình hành)
=> OB=OD. Mà BE=DF(gt)
=> OB-BE=OD-DF => OE=OF. Mà O nằm giữa E và F
=> O là trung điểm của EF
Xét tứ giác AECF có: AC cắt EF tại O
Mà O là trung điểm của AC( c/m trên )
O là trung điểm của EF( c/m trên )
=> AECF là hình bình hành (Tứ giác có 2 đ/c cắt nhau tại trung điểm của mỗi đg là hình bình hành)
b) Để AECF là hình thoi => \(AC\perp EF\) tại O
=> \(AC\perp BD\) tại O \(\left(E,F\in\left(O\right)\right)\)
Xét hình bình hành ABCD có: \(AC\perp BD\) tại O (c/m trên)
=> ABCD là hình thoi (Hình bình hành có 2 đ/c vuông góc là hình thoi)
Vậy để AECF là hình thoi thì ABCD là hình thoi
a) Vì ABCD là hình thoi(gt). Mà AC và BD cắt nhau tại O
=> O là trung điểm của AC và BD (t/c của hình bình hành)
=> OB=OD. Mà BE=DF(gt)
=> OB-BE=OD-DF => OE=OF. Mà O nằm giữa E và F
=> O là trung điểm của EF
Xét tứ giác AECF có: AC cắt EF tại O
Mà O là trung điểm của AC( c/m trên )
O là trung điểm của EF( c/m trên )
=> AECF là hình bình hành (Tứ giác có 2 đ/c cắt nhau tại trung điểm của mỗi đg là hình bình hành)
b) Để AECF là hình thoi => AC⊥EFAC⊥EF tại O
=> AC⊥BD tại O (E,F∈(O)
Xét hình bình hành ABCD có: AC⊥BDAC⊥BD tại O (c/m trên)
=> ABCD là hình thoi (Hình bình hành có 2 đ/c vuông góc là hình thoi)
Vậy để AECF là hình thoi thì ABCD là hình thoi

mik cho gợi ý thôi né :cậu c/m cho :
S2=S5 => S1=S4
Mà S tam giác ABM=S tam giác AMC=/2S tam giác ABC
C/m :S1+S2+S3 =S4+S5+S6=1/2 S tam giác ABC
=> Đpcm
Chúc bạn học tốt nha!