Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài toán 1: (Hình a)
Gọi đường thẳng qua N vuông góc với AN cắt AC tại R, qua P kẻ đường thẳng song song với BC. Đường thẳng này cắt AM,AN,BC lần lượt tại S,T,K.
Ta thấy \(\Delta\)APR có AN vừa là đường cao, đường phân giác => \(\Delta\)APR cân tại A => AP = AR, NP = NR
Áp dụng hệ quả ĐL Thales \(\frac{BM}{PS}=\frac{CM}{KS}\left(=\frac{AM}{AS}\right)\)=> PS = KS
Áp dụng ĐL đường phân giác trong tam giác: \(\frac{TK}{TP}=\frac{AK}{AP}\Rightarrow\frac{ST+SK}{TP}=\frac{AK}{AR}\)
\(\Rightarrow\frac{2ST+PT}{TP}=\frac{AR+RK}{AR}\Rightarrow\frac{2ST}{TP}=\frac{RK}{AR}\)
Dễ thấy NS là đường trung bình của \(\Delta\)RKP => RK = 2NS. Do đó \(\frac{ST}{TP}=\frac{NS}{AR}\)
Đồng thời NS // AR, suy ra \(\frac{ST}{TP}=\frac{NS}{AR}=\frac{SQ}{QA}\)=> QT // AP (ĐL Thaels đảo)
Mà AP vuông góc PO nên QT vuông góc PO. Từ đây suy ra T là trực tâm của \(\Delta\)POQ
=> QO vuông góc PT. Lại có PT // BC nên QO vuông góc BC (đpcm).
Bài toán 2: (Hình b)
Ta có IB = IC => \(\Delta\)BIC cân tại I => ^IBC = ^ICB = ^ACB/2 => \(\Delta\)MCI ~ \(\Delta\)MBC (g.g)
=> MC2 = MI.MB. Xét \(\Delta\)AHC có ^AHC = 900 , trung tuyến HM => HM = MC
Do đó MH2 = MI.MB => \(\Delta\)MIH ~ \(\Delta\)MHB (c.g.c) => ^MHI = ^MBH = ^MBC = ^MCI
=> Tứ giác CHIM nội tiếp. Mà CI là phân giác ^MCH nên (IH = (IM hay IM = IH (đpcm).
Bài toán 3: (Hình c)
a) Gọi đường thẳng qua C vuông góc CB cắt MK tại F, DE cắt BC tại Q, CG cắt BD tại I.
Áp dụng ĐL Melelaus:\(\frac{MB}{MC}.\frac{GA}{GB}.\frac{DC}{DA}=1\)suy ra \(\frac{DC}{DA}=2\)=> A là trung điểm DC
Khi đó G là trọng tâm của \(\Delta\)BCD. Do CG cắt BD tại I nên I là trung điểm BD
Dễ thấy \(\Delta\)BCD vuông cân tại B => BI = CM (=BC/2). Từ đó \(\Delta\)IBC = \(\Delta\)MCF (g.c.g)
=> CB = CF => \(\Delta\)BCF vuông cân ở C => ^CBA = ^CBF (=450) => B,A,F thẳng hàng
=> CA vuông góc GF. Từ đó K là trực tâm của \(\Delta\)CGF => GK vuông góc CF => GK // CM
Theo bổ đề hình thang thì P,Q lần lượt là trung điểm GK,CM. Kết hợp \(\Delta\)CEM vuông ở E
=> EQ=CM/2. Áp dụng ĐL Melelaus có \(\frac{GD}{GM}.\frac{EQ}{ED}.\frac{CM}{CQ}=1\)=> \(\frac{EQ}{ED}=\frac{1}{4}\)
=> \(\frac{ED}{CM}=2\)=> DE = 2CM = BC (đpcm).
b) Theo câu a thì EQ là trung tuyến của \(\Delta\)CEM vuông tại E => EQ = QC => ^QEC = ^QCE
Vì vậy ^PEG = ^QEC = ^QCE = ^PGE => \(\Delta\)EPG cân tại P => PG = PE (đpcm).


a) G là giao điểm của hai đường trung tuyến AM và BN nên G là trọng tâm tam giác ABC.
Suy ra: \(AG = 2GM\). Mà trên tia đối của tia MA lấy điểm D sao cho MD = MG nên \(GD = 2GM\).
Vậy GA = GD (= 2GM).
b) Xét hai tam giác MBG và MCD có:
MB = MC (M là trung điểm cạnh BC)
\(\widehat {GMB} = \widehat {DMC}\)(đối đỉnh)
GM = GD.
Vậy \(\Delta MBG = \Delta MCD\)(c.g.c).
c) \(\Delta MBG = \Delta MCD\) nên BG = CD (2 cạnh tương ứng).
Mà G là trọng tâm tam giác ABC nên \(BG = 2GN\). Mà BG = CD nên \(CD = 2GN\).

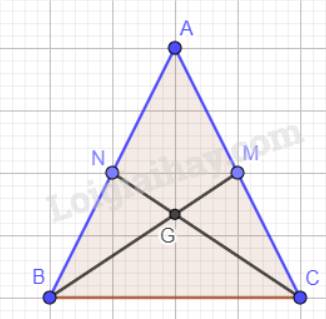
a) Tam giác ABC cân tại A nên AB = AC. M, N lần lượt là trung điểm của cạnh AC, AB nên AM = AN.
Xét tam giác ABM và tam giác ACN có: AM = AN; \(\widehat A\)chung; AB = AC.
Vậy \(\Delta ABM = \Delta ACN\)(c.g.c) hay BM = CN.
b) Xét tam giác ABC có G là giao điểm của hai đường trung tuyến BM và CN nên G là trọng tâm tam giác ABC. Do đó:
\(GB = \dfrac{2}{3}BM;GC = \dfrac{2}{3}CN\). Mà BM = CN nên GB = GC.
Vậy tam giác GBC cân tại G.

a: góc ABC=2/3*90=60 độ
góc ACB=90-60=30 độ
Xét ΔABD có
AH vừa là đường cao, vừa là trung tuyến
=>ΔABD cân tại A
mà góc B=60 độ
nên ΔABD đều
b: Xét ΔDAC có góc DAC=góc DCA
nên ΔDAC cân tại D
Xét ΔDHA vuông tại H và ΔDGC vuông tại G có
DA=DC
góc HDA=góc GDC
=>ΔDHA=ΔDGC
=>DH=DG và CG=AH
c: ΔBAD cân tại B
mà BM là trung tuyến
nên BM vuông góc AC
Xét ΔDBA có
BM,AH là đường cao
BM cắt AH tại E
=>E là trực tâm
=>DE vuông góc AB
=>DE//AC
a) Xét tam giác AHB và tam giác AHM có:
AH chung;
\(\widehat {AHB} = \widehat {AHM}\)(H là hình chiếu của A lên BC nên \(AH \bot BC\));
HB = HM (H là trung điểm của BM).
Vậy \(\Delta AHB = \Delta AHM\)(c.g.c).
b) \(\Delta AHB = \Delta AHM\)nên AB = AM ( 2 cạnh tương ứng).
G là giao điểm của hai đường trung tuyến AM và BN nên G là trọng tâm tam giác ABC. Nên: \(AG = \dfrac{2}{3}AM\).
Mà AB = AM suy ra: \(AG = \dfrac{2}{3}AB\).