Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Để chứng minh tứ giác ABDC là hình chữ nhật, ta cần chứng minh AB || CD và AB = CD.
Vì Bx vuông góc với AB, nên AB || Bx.
Vì Cy vuông góc với AC, nên AC || Cy.
Do đó, AB || CD.
Ta có:
- Góc ABC = 90 độ (vì tam giác ABC vuông tại A).
- Góc BAC = 90 độ (vì Bx vuông góc với AB).
- Góc ACB = 90 độ (vì Cy vuông góc với AC).
Vậy tứ giác ABDC có 4 góc vuông, tức là là hình chữ nhật.
b) Gọi M là điểm đối xứng của B qua A và N là điểm đối xứng của C qua A. Ta cần chứng minh tứ giác BCMN là hình thoi và AD = MC.
Vì M là điểm đối xứng của B qua A, nên AM = MB và góc AMB = góc BMA = 90 độ.
Vì N là điểm đối xứng của C qua A, nên AN = NC và góc ANC = góc CNA = 90 độ.
Do đó, ta có:
- AM = MB = MC (vì M là trung điểm của BC).
- AN = NC = NB (vì N là trung điểm của BC).
- Góc BMC = góc BMA + góc AMC = 90 độ + 90 độ = 180 độ (tổng các góc trong tứ giác là 360 độ).
Vậy tứ giác BCMN là hình thoi và AD = MC.
c) Gọi E là trung điểm của AC và F là trung điểm của MN. Ta cần chứng minh EF || ND.
Vì E là trung điểm của AC, nên AE = EC.
Vì F là trung điểm của MN, nên AF = FN.
Do đó, ta có:
- AE = EC = AF = FN.
- Góc AEF = góc AFE = góc NDF = góc NFD = 90 độ (vì E và F lần lượt là trung điểm của AC và MN).
Vậy EF || ND.

+ Xét tứ giác BHCD có
BD vuông góc AB; CH vuông góc AB => BD//CH (cùng vuôn góc AB) (1)
CD vuông góc AC; BH vuông góc AC => CD//BH (cùng vuông góc AC) (2)
Từ (1) và (2) => BHCD là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một)
+ Nối H với D cắt BC tại O'
=> O'B=O'C (t/c đường chéo hình bình hành) mà O là trung điểm BC => O trùng O' => H; O; D thẳng hàng

a: Xét tứ giác BHCD có
BH//CD
CH//BD
DO đó: BHCD là hình bình hành
Câu b và c sai đề rồi bạn

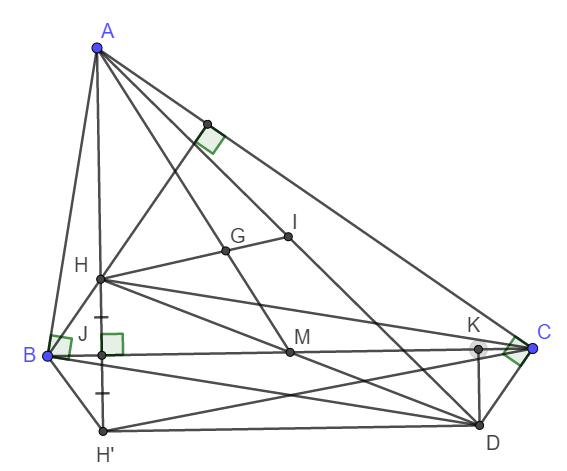
a) Ta thấy H là trực tâm tam giác ABC nên CH vuông góc AB. Suy ra DB song song CH.
Tương tự BH song song DC (Cùng vuông góc AC)
Vậy nên tứ giác BHCD là hình bình hành.
Do BHCD là hình bình hành nên \(\Delta BHC=\Delta CDB\left(c-g-c\right)\)
Lại có H' đối xứng với H qua BC nên \(\Delta BHC=\Delta BH'C\left(c-c-c\right)\)
Vậy thì \(\Delta CDB=\Delta BH'C\)
Gọi J là giao điểm của HH' và BC. Kẻ DK vuông góc BC tại K.
Khi đó ta có ngay H'J = KD. Vậy nên JKDH' là hình bình hành hay JK//H'D
Suy ra tứ giác BCDH' là hình thang.
Lại có : H'C = BD (Cùng bằng HC) nên BCDH' là hình thang cân.
b) Do BHCD là hình bình hành nên giao điểm của HD và BC là trung điểm mỗi đường. Ta gọi điểm đó là M.
Xét tam giác AHD có AM là trung tuyến, \(AG=\frac{2}{3}AM\) nên G là trọng tâm tam giác.
Vậy thì HG đi qua trung điểm AD, hay H, G, I thẳng hàng.
d) Để hình bình hành BHCD là hình thoi thì BH = HC. Vậy thì AH là đường cao đồng thời trung trực nên tam giác ABC là tam giác cân tại A.
Để hình bình hành BHCD là hình chữ nhật thì HC vuông góc BH. Lại có HC//BD nên BD//BH. Vậy thì BH trùng AB. Tương tự CH trùng AC.
Suy ra để BHCD là hình chữ nhật thì tam giác ABC vuông tại A.

