
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(BH\cdot BC=AB^2\left(1\right)\)
Xét ΔBDC vuông tại B có BA là đường cao ứng với cạnh huyền DC
nên \(AD\cdot AC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BH\cdot BC=AD\cdot AC\)

Đặt BH = x
=> BC = x + 4
Tam giác ABH vuông tại H , theo HTL :
AB^2 = BH.BC
<=> 4^2 = x(x+4)
<=> x^2 + 4x - 16 = 0
<=> x^2 + 4x + 4 - 20 = 0
<=> ( \(\left(x+2+2\sqrt{5}\right)\left(x+2-2\sqrt{5}\right)\) = 0
=> \(x=2\sqrt{5}-2\) ( vì x >0 )
AC^2 = HC.BC = 4.\(\left(2\sqrt{5}-2+4\right)=4.\left(2\sqrt{5}+2\right)=8\sqrt{5}+8\)
AM = 1/2BC = \(\frac{1}{2}\left(2\sqrt{5}-2+4\right)=\frac{1}{2}\left(2\sqrt{5}+2\right)=\sqrt{5}+1\)

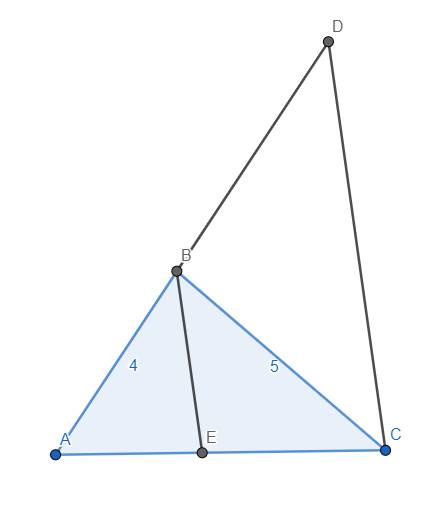
a) Xét tam giác ACB và ADC, có \(\widehat{A}\) chung và \(\widehat{ACB}=\widehat{ADC}\left(gt\right)\), suy ra đpcm.
b) Từ câu a) \(\Rightarrow\dfrac{AB}{AC}=\dfrac{AC}{AD}\) \(\Rightarrow AC^2=AB.AD\)
Kẻ phân giác BE của tam giác ABC. Vì \(\widehat{B}=2\widehat{C}\) nên \(\widehat{ABE}=\widehat{ADC}\) hay BE//CD. Mặt khác, \(\dfrac{EA}{EC}=\dfrac{BA}{BC}=\dfrac{4}{5}\) nên suy ra \(\dfrac{BA}{BD}=\dfrac{4}{5}\Leftrightarrow\dfrac{4}{BD}=\dfrac{4}{5}\Leftrightarrow BD=5\), suy ra \(AD=AB+BD=4+5=9\).
\(\Rightarrow AC^2=AB.AD=4.9=36\) \(\Rightarrow AC=6\).
Vậy \(AC=6\)
Dạ thưa cô, cái này em áp dụng tính chất đường phân giác trong tam giác ạ. Cái này lớp 9 được dùng luôn không cần chứng minh ạ.

góc C=180-30-80=70 độ
Xét ΔABC có
AB/sinC=AC/sinB=BC/sinA
=>3/sin70=AC/sin80=BC/sin30
=>\(BC\simeq1,6\left(cm\right);AC\simeq3,14\left(cm\right)\)

Lời giải:
Xét tam giác vuông $ABH$:
$\frac{AH}{AB}=\sin B\Rightarrow AH=AB.\sin B=12.\sin 40^0=12\sin 40^0=7,71$ (cm)
Xét tam giác vuông $AHC$:
$\frac{AH}{AC}=\sin C\Rightarrow AC=\frac{AH}{\sin C}=\frac{7,71}{\sin 30^0}=15,42$ (cm)