
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: M là trung điểm của BC
=>AM là đường trung tuyến của ΔABC
b: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
=>ΔABM=ΔACM
=>góc BAM=góc CAM
=>AM là phân giác của góc BAC
c: Sửa đề; tam giác ABC
AB=AC
BM=CM
=>AM là trung trực của BC

Tham khảo:

Xét tam giác ABM và tam giác ACM có :
AM chung
BM = CM ( M là trung điểm BC )
AB = AC (tam giác ABC cân tại A theo giả thiết)
\( \Rightarrow \Delta AMB = \Delta AMC (c-c-c)\)
\( \Rightarrow \widehat{BAM}= \widehat{CAM}\) (2 góc tương ứng)
\( \Rightarrow \) AM thuộc tia phân giác của góc A
Mà AM cắt tia phân giác góc B tại I
\( \Rightarrow \) I là giao của các đường phân giác trong tam giác ABC
\( \Rightarrow \) CI là phân giác góc C (định lí 3 đường phân giác cắt nhau tại 1 điểm)

1/Giả sử trong 1 tam giác có 2 hóc tù thì tổng 3 góc của tam giác đó sẽ lớn hơn 180 độ
=>trong 1 tam giác chỉ có duy nhất 1 góc tù
2/Trong 1 tam giác nếu góc nhỏ nhất bằng 60 độ thì tổng 3 góc của tam giác đó sẽ lớn hơn 180 độ
=> trong một tam giác góc nhỏ nhất không thể lớn hơn 60 độ
3/Xét tam giác AMB = tam giác AMC (c.c.c)
=> góc BMA = góc CMA
Mặt khác góc BMA + góc CMA = 180 độ
=> góc BMA = góc CMA = 90 độ
=> AM vuông góc BC
=> AM là đường cao của tam giác hạ từ đỉnh A
Tam giác BMA = tam giác CMA
=> góc BAM = góc CAM
=> AM là tia phân giác của góc A

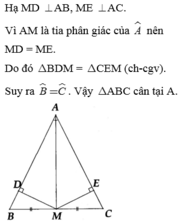
a: 
b: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
=>ΔABM=ΔACM
=>góc BAM=góc CAM
=>AM là phân giác của góc BAC

#\(N\)
`a,` Vì Tam giác `ABC` cân tại `A -> AB = AC, `\(\widehat{B}=\widehat{C}\)
`AM` là đường trung tuyến Tam giác `ABC -> BM = MC`
Xét Tam giác `ABM` và Tam giác `ACM` có:
`AB = AC`
\(\widehat{B}=\widehat{C}\)
`BM = MC`
`->` Tam giác `ABM =` Tam giác `ACM (c-g-c)`
`->`\(\widehat{BAM}=\widehat{CAM}\) `(2` góc tương ứng `)`
`-> AM` là phân giác của \(\widehat{BAC}\)
Xét tam giác \(\Delta ABM\) và \(\Delta ACM\)
\(AB=AC\left(gt\right)\)
\(\widehat{ABM}=\widehat{ACM}\left(gt\right)\)
\(AM\) chung
\(\Rightarrow\Delta ABM=\Delta ACM\left(c.g.c\right)\)
Từ tam giác bằng nhau trên suy ra:
\(\widehat{BAM}=\widehat{CAM}\) nên \(AM\) là phân giác \(\widehat{BAC}\)
Là phân giác của \(\Delta ABC\)

câu 2 :
a) có phải là chứng minh AM ⊥ BC không
xét ΔAMB và ΔAMC, ta có :
AB = AC (2 cạnh bên của ΔABC cân tại A)
MB = MC (AM là đường trung tuyến của cạnh BC)
AM là cạnh chung
=> ΔAMB = ΔAMC (c.c.c)
=> \(\widehat{AMB}=\widehat{AMC}\) (2 cạnh tương ứng)
mà \(\widehat{AMB}+\widehat{AMC}=180^O\) (kề bù)
\(\Rightarrow\widehat{AMB}=\widehat{AMC}=\dfrac{180^O}{2}=90^O\)
=> AM ⊥ BC