Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\cos ABC=\dfrac{BA^2+BC^2-AC^2}{2\cdot BA\cdot BC}\)
\(\Leftrightarrow89a^2-AC^2=2\cdot5a\cdot8a\cdot\dfrac{1}{2}=40a^2\)
=>AC=7a
\(AM=\dfrac{b^2+c^2}{2}-\dfrac{a^2}{4}=\dfrac{25a^2+49a^2}{2}-\dfrac{64a^2}{4}=37a^2-16a^2=21a^2\)
hay \(AM=a\sqrt{21}\left(cm\right)\)

Áp dụng định lý hàm cosin:
\(AC=\sqrt{AB^2+BC^2-2AB.BC.cosB}=\sqrt{2^2+3^2-2.2.3.cos60^0}=\sqrt{2}\)
Diện tích tam giác:
\(S=\dfrac{1}{2}AB.BC.sinB=\dfrac{1}{2}.2.3.sin60^0=\dfrac{3\sqrt{3}}{2}\)

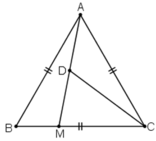
a) Do tam giác ABC là tam giác đều nên 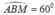 .
.
Theo định lý côsin trong tam giác ABM ta có:

b) Theo định lý sin trong tam giác ABM ta có:
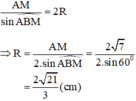
c) Ta có: BM + MC = BC nên MC = BC – BM = 6 - 2 = 4 cm.
Gọi D là trung điểm AM.
Áp dụng công thức độ dài đường trung tuyến trong tam giác ta có:
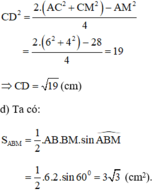

a: vecto AB=(1;2)
vecto BC=(3;-2)
vecto AC=(4;0)
b: Tọa độ I là:
x=(-1+0)/2=-1/2 và y=(2+4)/2=3
Tọa độ G là:
\(\left\{{}\begin{matrix}x=\dfrac{-1+0+3}{3}=\dfrac{2}{3}\\y=\dfrac{2+4+2}{3}=\dfrac{8}{3}\end{matrix}\right.\)
c: vecto AB=(1;2); vecto BC=(3;-2); vecto AC=(4;0)
A(-1;2); B(0;4); C(3;2)
PTTS của AB là:
x=-1+t và y=2+2t
PTTS của AC là:
x=-1+4t và y=2+0t=2
PTTS của BC là;
x=3+4t và y=2+0t=2
vecto AB=(1;2)
=>VTPT là (-2;1)
PTTQ của AB là:
-2(x+1)+1(y-2)=0
=>-2x-2+y-2=0
=>-2x+y-4=0
vecto AC=(4;0)
=>VTPT là (0;-4)
Phương trình AC là:
0(x-3)+(-4)(y-2)=0
=>y=2
Ta có: DE đi qua trung điểm của AB và BC
⇒ DE là đường trung bình của tam giác ABC:
\(DE=\dfrac{1}{2}AC\)
\(\Rightarrow AC=DE:\dfrac{1}{2}=3:\dfrac{1}{2}=6\)
Áp dụng định lý cosin ta có:
\(AB^2=AC^2+BC^2-2\cdot AC\cdot BC\cdot cosACB\)
\(\Rightarrow9^2=6^2+BC^2-2\cdot6\cdot BC\cdot cos60^o\)
\(\Rightarrow81=36+BC^2-6BC\)
\(\Rightarrow BC^2-6BC-45=0\)
\(\Delta=\left(-6\right)^2-4\cdot1\cdot\left(-45\right)=216\)
\(\Rightarrow\left[{}\begin{matrix}BC=\dfrac{6+6\sqrt{6}}{2}=3+3\sqrt{6}\left(tm\right)\\BC=\dfrac{6-6\sqrt{6}}{2}=3-3\sqrt{6}\left(ktm\right)\end{matrix}\right.\)
\(\Rightarrow BC=3+3\sqrt{6}\)