Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C M N I K'
a) Ta có: AC=AN+NC=12,5
=> \(\frac{AN}{AC}=\frac{7,5}{12,5}=\frac{3}{5}=\frac{AM}{AB}\)
Theo định lí Talet => MN//BC
b) Với I là trung điểm MN , Gọi K' là giao điểm của AI và BC ta chứng minh K' trùng với K
Vì MN//BC nên ta có: \(\frac{MI}{BK'}=\frac{IN}{K'C}\left(=\frac{AI}{AK'}\right)\)
Mà MI=IN (I là trung điểm )=> BK'=K'C , K' thuộc BC => K' là trung điểm BC theo đề bài K cũng là trung điểm BC => K' trùng K
=> A, I, K thẳng hàng

A B C N K M
a, Ta có :
\(\frac{AM}{MB}=\frac{3}{2},\frac{AN}{NC}=\frac{7,5}{5}=\frac{3}{2}\Rightarrow\frac{AM}{MB}=\frac{AN}{NC}\left(=\frac{3}{2}\right)\)
=> MN // BC ( định lí Talet đảo )
b, Ta có :
\(K\in MN;I\in BC\Rightarrow NK//CI;KM//BI\)
\(\Rightarrow\frac{NK}{CI}=\frac{AK}{AI},\frac{KM}{IB}=\frac{AK}{AI}\)
\(\Rightarrow\frac{NK}{CI}=\frac{KM}{IB}\left(=\frac{AK}{AI}\right)\)
Mà \(CI=IB\Rightarrow NK=KM\)
Vậy : K là trung điểm của NM

Xét tam giác ABC, có:
* D, E lần lượt là trung điểm của AB, AC (gt)
=> DE là đường trung bình của tam giác ABC
=> DE // BC
=> DE = 1/2 BC = 1/2 . 8 = 4 (cm)
Ta có: DE // BC (cmt)
=> DECB là hình thang
Xét hình thang DECB (DE // BC), có:
* M, N lần lượt là trung điểm của DB, EC (gt)
=> MN là đường trung bình của hình thang DECB
=> MN = (DE + BC) : 2 = (4+8) : 2 = 6 (cm)
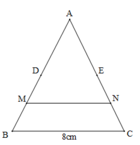
Cho tam giác ABC có BC = 8cm. Gọi D và E lần lượt là trung điểm các cạnh AB, AC. M và N lần lượt là trung điểm của BD và CE. Khi đó MN =.........cm
Xét tam giác ABC, có:
* D, E lần lượt là trung điểm của AB, AC (gt)
=> DE là đường trung bình của tam giác ABC
=> DE // BC
=> DE = 1/2 BC = 1/2 . 8 = 4 (cm)
Ta có: DE // BC (cmt)
=> DECB là hình thang
Xét hình thang DECB (DE // BC), có:
* M, N lần lượt là trung điểm của DB, EC (gt)
=> MN là đường trung bình của hình thang DECB
=> MN = (DE + BC) : 2 = (4+8) : 2 = 6 (cm)
nhé !

A B C M N 3 5 10 16 6
Ta có: \(\frac{MB}{AB}=\frac{MB}{AM+MB}=\frac{5}{8}\)
\(\frac{NC}{AC}=\frac{10}{16}=\frac{5}{8}\)
=> \(\frac{MB}{AB}=\frac{NC}{AC}\)Theo định lí Ta-lét đảo
=> MN // BC
Áp dụng hệ quả định lí Ta-lét vào \(\Delta ABC\)có MN // BC
=> \(\frac{MN}{BC}=\frac{AM}{AB}\)=> \(BC=\frac{MN.AB}{AM}=\frac{8.6}{3}=16\)

ChọnB