K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
NL
nguyen luong
22 tháng 4 2018 - olm

Cho tam giác ABC có AB = 4 cm, AC = 3 cm, BC = 5 cm.
a) Chứng minh : tam giác ABC vuông
b) Trên AB lấy D sao cho AD = 3 cm. Chứng minh góc ACD = góc ADC
c) Tia phân giác góc CAD cắt BC tại M. So sánh MC và MD ?
d) Cho AM cắt CD tại K. Chứng minh AK < \(\frac{CB}{2}\)
#Toán lớp 7
0
T
tủn
29 tháng 4 2019 - olm

Cho DABC có AB = 3 cm; AC = 4 cm; BC = 5 cm.

a) Chứng tỏ tam giác ABC vuông tại A.

b)Vẽ phân giác BD (D thuộc AC), từ  D vẽ \(DE\perp BC\) (\(E\in BC\)). Chứng minh DA = DE.

c) ED cắt AB tại F. Chứng minh \(\Delta ADF=\Delta EDC\)
#Toán lớp 7
3
ND
nguyen duc thang
29 tháng 4 2019

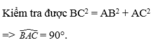
Hình tự vẽ nha 

a ) Vì AB = 3 ( gt ) => AB2 = 9

          AC = 4 ( gt ) => AC2 = 16

          BC = 5 ( gt ) => BC2 = 25

MÀ 25 = 9 + 16

DO đó BC2 = AB2 + AC2

=> \(\Delta\)ABC vuông tại A ( định lí đảo định lí py ta go )

Vậy  \(\Delta\)ABC vuông tại A

Đúng(0)
ND
nguyen duc thang
29 tháng 4 2019

b ) Vì  \(\Delta\)ABC vuông tại A ( CM a ) => BAC = 90o hay BAD = 90o

Vì DE \(\perp\)BC ( gt ) => BED = DEC = 90o ( định nghĩa 2 đường thẳng vuông góc )

Vì BD là tia phân giác  của góc B ( gt ) => ABD = EBD 

Xét  \(\Delta\)ABD và \(\Delta\)EBD có :

ABD = EBD ( cmt )

BD chung

BAD = BED ( = 90o )

DO đó \(\Delta\)ABD = \(\Delta\)EBD ( cạnh huyền - góc nhọn )

=> DA = DE ( 2 cạnh tương ứng )

Vậy ..

Đúng(0)
TT
Trần Trường Nguyên
19 tháng 4 2022 - olm

Cho ABC có AB = 3 cm; AC = 4 cm; BC = 5 cm. a) Chứng tỏ tam giác ABC vuông tại A. b)Vẽ phân giác BD (D thuộc AC), từ D vẽ DE  BC (E  BC). Chứng minh DA = DE. c) ED cắt AB tại F. Chứng minh ADF = EDC rồi suy ra DF > DE.
#Toán lớp 7
0
ND
Nguyễn Diệu Linh
16 tháng 3 2022 - olm
Bài 2: Cho tam giác ABC có góc A>90 độ , lấy điểm M thuộc cạnh AB .a) So sánh AC và MC b) Chứng minh tam giác MBC là tam giác tùc) Chứng minh AC <MC <BCBài 3: Cho tam giác MNP có Góc N>90 độ , trên tia đối của tia NP lấy điểm Q .a) So sánh MN và MP b) Chứng minh tam giác MPQlà tam giác tù.c) Chứng minh MN<MP<MQBài 4: Cho tam giác ABC có AB=3 cm, AC=4 cma) So sánh góc B với gócCb) Hạ AH vuông góc với BC tại H . So sánh góc...
Đọc tiếp

Bài 2: Cho tam giác ABC có góc A>90 độ , lấy điểm M thuộc cạnh AB .
a) So sánh AC và MC 
b) Chứng minh tam giác MBC là tam giác tù
c) Chứng minh AC <MC <BC
Bài 3: Cho tam giác MNP có Góc N>90 độ , trên tia đối của tia NP lấy điểm Q .
a) So sánh MN và MP 
b) Chứng minh tam giác MPQlà tam giác tù.
c) Chứng minh MN<MP<MQ
Bài 4: Cho tam giác ABC có AB=3 cm, AC=4 cm
a) So sánh góc B với gócC
b) Hạ AH vuông góc với BC tại H . So sánh góc BAH và góc CAH
Bài 5: Cho tam giác ABC có AB = 5 cm, AC = 3 cm
a) So sánh góc B với góc C
b) So sánh hai góc ngoài tại các đỉnh B và C của tam giác ABC
Bài 6: Cho tam giác ABC vuông tại A có AC=2AB . Lấy điểm E trên cạnh AC sao cho
AB=AE . Trên tia đối của tia EB lấy điểm D sao cho EB=ED
a) Chứng minh tam giác ABE= tam giác CDE 
b) So sánh góc ABE  và góc CBE
#Toán lớp 7
0
L
linh
21 tháng 7 2015 - olm

Cho tam giác ABC VÀ AB=6 cm, BC=10 cm, góc A =90•

a) tính AC

B) Kẻ AH vuông góc BC, HK vuông góc vs CB, HI VUÔNG GÓC VS AB . Chứng minh HI=AR

c) tính chu vi và diện tích của tam giác ABC 
#Toán lớp 7
0
DA
Diệu Anh Hoàng
6 tháng 1 2018 - olm

Cho tam giác ABC có BC= 52 cm, AB= 20 cm, AC= 48 cm. Chứng minh rằng:

a) Tam giác ABC vuông

b) Kẻ AH\(\perp\)BC, H\(\in\)BC. Tính độ dài AH.
#Toán lớp 7
0
NC
Nguyễn Cảnh Tùng
21 tháng 5 2019 - olm

Cho tam giác ABC có góc A = 90o và AB = 4 cm, BC = 5 cm

a) Tính AC

b) Trên tia đối của tia AB lấy điểm D sao cho AD = AB. CMR tam giác ABC = tam giác ADC

c) Trên AC lấy điểm E sao cho AE = \(\frac{1}{3}\)AC. CMR: DE đi qua trung điểm I của BC

d) CMR: 2 DI + 3 DC > 2 DB
#Toán lớp 7
3
D
阮草~๖ۣۜDαɾƙ
21 tháng 5 2019

a. Theo định lí Pitago:

Ta có: AB2 + AC2 = BC2

           42    + AC2 = 52

           16    + AC2 = 25

                      AC2 = 25 - 16

                      AC2 = 9

                       AC2 = 33

              =>       AC   = 3 (cm)

Đúng(0)
D
阮草~๖ۣۜDαɾƙ
21 tháng 5 2019

A B C D E

Đúng(0)
BP
Bùi Phương Thu
27 tháng 4 2016 - olm

Cho ABC có AB = 3 cm; AC = 4 cm; BC = 5 cm.

a) Chứng tỏ tam giác ABC vuông tại A.

b)Vẽ phân giác BD (D thuộc AC), từ  D vẽ DE vuông góc với  BC (E thuộc  BC).

Chứng minh DA = DE.

c) ED cắt AB tại F. Chứng minh tam giác ADF = tam giác EDC rồi suy ra DF > DE.

 

 
#Toán lớp 7
1
DN
Đức Nguyễn Ngọc
27 tháng 4 2016

a) Ta có: \(BC^2=AB^2+AC^2\) (do \(5^2=4^2+3^2\) )

\(\Rightarrow\Delta ABC\) vuông tại A

b) Xét 2 tam giác vuông BDA và BDE, có:

Góc ABD = góc EBD (phân giác BD của góc B)

BD là cạnh chung

\(\Rightarrow\) \(\Delta\) vuông BDA = \(\Delta\) vuông BDE(cạnh huyền - góc nhọn)

\(\Rightarrow\) DA = DE(2 cạnh tương ứng)

c) Xét 2 tam giác vuông ADF và EDC, ta có:

DA = DE (chứng minh a)

 góc ADF = góc EDC (đối đỉnh)

\(\Rightarrow\Delta\) vuông ADF = \(\Delta\) vuông EDC (cạnh góc vuông - góc nhọn)

Ta có: \(\Delta\)ADF là tam giác vuông tại A 

\(\Rightarrow\) DF là cạnh huyền của tam giác ADF

\(\Rightarrow\) DF > DA

Mà DE = DA (\(\Delta ADF=\Delta EDC\) )

nên DF > DE

Đúng(1)
KT
Kammy TV
27 tháng 2 2020

Cho tam giác ABC có AB bằng 3 cm , AC bằng 4 cm , BC = 5 cm . Chứng minh góc BAC bằng 90 độ

#Toán lớp 7
1
A
💋Amanda💋
27 tháng 2 2020
https://i.imgur.com/MG6g3oN.jpg
Đúng(0)
KT
Kammy TV
27 tháng 2 2020

Thank

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP