Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
cho điểm A(1;2) B(-2;6) C(9;8) . Tìm tọa độ điểm k trên trục Ox để tu giác AOBK là hình thang đáy AO


a: \(AB=\sqrt{\left(-2-1\right)^2+\left(6-2\right)^2}=5\)
\(AC=\sqrt{\left(9-1\right)^2+\left(8-2\right)^2}=10\)
\(BC=\sqrt{\left(9+2\right)^2+\left(8-6\right)^2}=5\sqrt{5}\)
Vì AB^2+AC^2=BC^2
nên ΔABC vuông tại A
b: \(cosB=\dfrac{AC}{BC}=\dfrac{10}{5\sqrt{5}}=\dfrac{2}{\sqrt{5}}\)
c: Hình chiếu của A trên AB là A
c: \(S_{ABC}=\dfrac{1}{2}\cdot5\cdot10=25\)

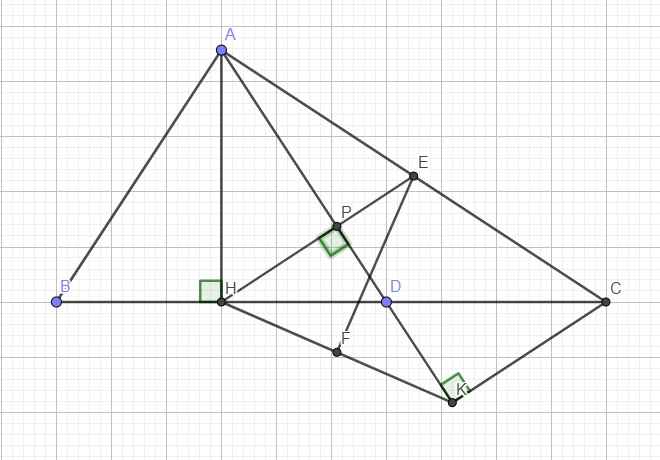
Gọi E là trung điểm AC, do H và K cùng nhìn AC dưới 1 góc vuông nên H, K thuộc đường tròn đường kính AC (1)
\(\Rightarrow EH=EK\) hay E nằm trên trung trực HK
Gọi F là trung điểm HK \(\Rightarrow F\left(2;-1\right)\)
\(\overrightarrow{HK}=\left(14;-8\right)=2\left(7;-4\right)\Rightarrow\) EF nhận (7;-4) là 1 vtpt
Phương trình EF: \(7\left(x-2\right)-4\left(y+1\right)=0\Leftrightarrow7x-4y-18=0\)
Tọa độ E là nghiệm: \(\left\{{}\begin{matrix}x-y+10=0\\7x-4y-18=0\end{matrix}\right.\) \(\Rightarrow E\left(\dfrac{58}{3};\dfrac{88}{3}\right)\)
\(\widehat{ACH}=\widehat{HAK}\) (cùng phụ \(\widehat{ABC}\)) \(\Rightarrow AH=HK\)
Mà \(AE=EK\) theo (1) \(\Rightarrow AK\) là trung trực EH
\(\overrightarrow{HE}=\left(\dfrac{73}{3};\dfrac{103}{3}\right)=\dfrac{1}{3}\left(73,103\right)\) \(\Rightarrow AK\) nhận \(\left(103;-73\right)\) là 1 vtpt
Tới đây bạn hãy kiểm tra lại số liệu, số liệu quá bất hợp lý
Tính tiếp như sau:
Viết pt AK (biết đi qua K và có vtpt như trên)
Tìm tọa độ giao điểm P của EH và AK
Khi đó P là trung điểm AK, tìm tọa độ A dễ dàng bằng công thức trung điểm

a: N thuộc Ox nên N(x;0)
\(NA=\sqrt{\left(1-x\right)^2+\left(2-0\right)^2}=\sqrt{\left(x-1\right)^2+4}\)
\(NC=\sqrt{\left(9-x\right)^2+\left(8-0\right)^2}=\sqrt{\left(x-9\right)^2+64}\)
Để NA=NC thì (x-9)^2+64=(x-1)^2+4
=>x^2-18x+81+64-x^2+2x-1-4=0
=>-16x+140=0
=>x=8,75
b: K thuộc Ox nên K(x;0)
\(\overrightarrow{AO}=\left(1;2\right)\)
\(\overrightarrow{BK}=\left(x+2;-6\right)\)
Để AOKB là hình thang có hai đáy là AO và KB thì \(\dfrac{x+2}{1}=\dfrac{-6}{2}=-3\)
=>x+2=-3
=>x=-5

Đặt \(\overrightarrow{PB}=x\overrightarrow{BC}\)
\(\overrightarrow{PM}=\overrightarrow{PB}+\overrightarrow{BM}=x.\overrightarrow{BC}-\dfrac{1}{3}\overrightarrow{AB}\)
\(\overrightarrow{PN}=\overrightarrow{PC}+\overrightarrow{CN}=\left(x+1\right)\overrightarrow{BC}-\dfrac{1}{2}\overrightarrow{AC}=\left(x+1\right)\overrightarrow{BC}-\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{BC}\right)\)
\(=\left(x+\dfrac{1}{2}\right)\overrightarrow{BC}-\dfrac{1}{2}\overrightarrow{AB}\)
P, M, N thẳng hàng \(\Rightarrow\dfrac{x+\dfrac{1}{2}}{x}=\dfrac{\dfrac{1}{2}}{\dfrac{1}{3}}\Rightarrow x=1\) \(\Rightarrow\overrightarrow{PB}=\overrightarrow{BC}\)
\(\Rightarrow\) B là trung điểm PC \(\Rightarrow P\left(-6;5\right)\)
Nếu bạn chưa học bài pt đường thẳng thì làm cách trên, còn học rồi thì đơn giản là thiết lập 2 pt đường thẳng BC và MN là xong
\(\overrightarrow{AH}=\left(x_H-1;y_H-2\right)\)
\(\overrightarrow{BC}=\left(11;2\right)\)
\(\overrightarrow{BH}=\left(x_H+2;y_H-6\right)\)
Theo đề, ta có:
\(\left\{{}\begin{matrix}11x_H-11+2y_H-4=0\\2x_H+4-11y_H+66=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}22x_H+4y_H=30\\22x_H-121y_H=-770\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}125y_H=800\\11x_H+2y_H=15\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y_H=\dfrac{32}{5}\\x_H=\dfrac{1}{5}\end{matrix}\right.\)
cái khúc từ đề bài ta có xuống í, làm sao bạn ra được cái hệ phương trình đó vậy ạ?