Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

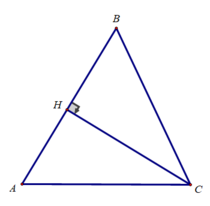
Kẻ đường cao CH của tam giác ABC. Ta có:
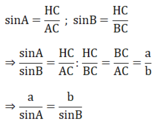
Chứng minh tương tự ta có:
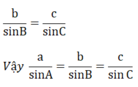

Tự vẽ hình
Kẻ BH \(\perp\)AC và \(CK\perp\)AB
Tam giác AKC vuông tại K
=>CK=bsinA (1)
Tam giác BKC vuông tại K
=>CK=asinB (2)
Từ (1) (2)=>bsinA=asinB
<=>\(\frac{a}{sinA}=\frac{b}{sinB}\)
Chứng minh tương tự ta có :\(\frac{a}{sinA}=\frac{c}{sinC}\)
Vậy ....

\(a,\) Kẻ \(BH\perp AC;CK\perp AB\)
\(\Delta ACK\) vuông tại K có \(CK=b\cdot\sin A\)
\(\Delta BKC\) vuông tại H có \(CK=a\cdot\sin B\)
\(\Rightarrow b\cdot\sin A=a\cdot\sin B\\ \Rightarrow\dfrac{a}{\sin A}=\dfrac{b}{\sin B}\left(1\right)\)
Cmtt ta được \(a\cdot\sin C=c\cdot\sin A\left(=BH\right)\)
\(\Rightarrow\dfrac{a}{\sin A}=\dfrac{c}{\sin C}\left(2\right)\)
\(\left(1\right)\left(2\right)\RightarrowĐpcm\)
\(b,\) Không thể suy ra đẳng thức

Kẻ AH vuông góc BC
Xét ΔAHB vuông tại H có sin B=AH/AB
=>AH=c*sin B
Xét ΔAHC vuông tại H có sin C=AH/AC
=>AH=AC*sin C=b*sin C
=>c*sin B=b*sin C
=>c/sinC=b/sinB
Kẻ BK vuông góc AC
Xét ΔABK vuông tại K có
sin A=BK/AB
=>BK=c*sinA
Xét ΔBKC vuông tại K có
sin C=BK/BC
=>BK/a=sin C
=>BK=a*sin C
=>c*sin A=a*sin C
=>c/sin C=a/sin A
=>a/sin A=b/sinB=c/sinC

a) Ta có: \(bc.sinA=ca.sinB=ab.sinC\left(=2S_{ABC}\right)\Rightarrow b.sinA=a.sinB;c.sinB=b.sinC\Rightarrow\frac{a}{sinA}=\frac{b}{sinB};\frac{b}{sinB}=\frac{c}{sinC}\Rightarrowđpcm\)
b) Ta có: \(a+b=2c\Leftrightarrow\frac{a}{c}+\frac{b}{c}=2\).
Từ câu a ta suy ra \(\frac{a}{c}=\frac{sinA}{sinC};\frac{b}{c}=\frac{sinB}{sinC}\).
Do đó: \(\frac{sinA}{sinC}+\frac{sinB}{sinC}=2\Rightarrow sinA+sinB=2sinC\) (đpcm).

Tự vẽ hình
Kẻ BH \(\perp\)AC và \(CK\perp\)AB
Tam giác AKC vuông tại K
=>CK=bsinA (1)
Tam giác BKC vuông tại K
=>CK=asinB (2)
Từ (1) (2)=>bsinA=asinB
<=>\(\frac{a}{sinA}=\frac{b}{sinB}\)
Chứng minh tương tự ta có :\(\frac{a}{sinA}=\frac{c}{sinC}\)
Vậy ....