Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔAMB và ΔCMD có
MA=MC
\(\widehat{AMB}=\widehat{CMD}\)(hai góc đối đỉnh)
MB=MD
Do đó: ΔAMB=ΔCMD
b: ta có: ΔAMB=ΔCMD
=>\(\widehat{MAB}=\widehat{MCD}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CD
c: Xét ΔIBM và ΔKDM có
IB=KD
\(\widehat{IBM}=\widehat{KDM}\)(hai góc so le trong, AB//CD)
BM=MD
Do đó: ΔIBM=ΔKDM
=>\(\widehat{IMB}=\widehat{KMD}\)
mà \(\widehat{IMB}+\widehat{IMD}=180^0\)(hai góc kề bù)
nên \(\widehat{KMD}+\widehat{IMD}=180^0\)
=>I,M,K thẳng hàng

UKM THÌ CÓ BÀI TỰA VẬY BẠN SO ĐC CHỨ
a) Xét AIM và BIC có:IA = IB (do I là trung điểm của AB);AIM BIC(hai góc đối đỉnh);IM = IC (giảthiết).Do đó AIM = BIC (c.g.c)Suy ra AM = BC (hai cạnh tương ứng) và MAI CBI(hai góc tương ứng) Mà MAI, CBIlà hai góc ởvịtrí so le trong nên AM // BC.b) Xét ANE và CBE có:EA = EC (do E là trung điểm của AC);AEN CEB(hai góc đối đỉnh);EN= EB(giảthiết).Do đó ANE = CBE (c.g.c)Suy ra NAE BCE(hai góc tương ứng)Mà NAE, BCElà hai góc ởvịtrí so le trong nên AN// BC.c) Ta có AM // BC (theo câu a) và AN // BC (theo câu b)Do đó qua điểm A có hai đường thẳng song song với BC nên theo tiên đềEuclid, hai đường thẳng AM và AN trùng nhau hay ba điểm A, M, N thẳng hàng.Lại có ANE = CBE (theo câu b) nên AN = CB (hai cạnh tương ứng)Mặt khác AM = BC (theo câu a)Do đó AM = AN (cùng bằng BC) Mà ba điểm A, M, N thẳng hàng nên A là trung điểm của MN.a: Xét ΔAMB và ΔCMD có
MA=MC
góc AMB=góc CMD
MB=MD
Do đó: ΔAMB=ΔCMD
b: Xét tứ giác ABCD có
M là trung điểm chung của AC và BD
nên ABCD là hình bình hành
=>AB//CD và AB=CD
c: Xét tứ giác AKBC có
N là trung điểm chung của AB và KC
nên AKBC là hình bình hành
=>AK//BC
mà AD//BC
nên D,A,K thẳng hàng

a: Xét ΔAMB và ΔCMD có
MA=MC
\(\widehat{AMB}=\widehat{CMD}\)
MB=MD
Do đó: ΔAMB=ΔCMD
b: Xét tứ giác ABCD có
M la trung điểm của AC
M là trung điểm của BD
DO đó: ABCD là hình bình hành
Suy ra: AB//CD và AB=CD

a: Xét ΔAMB và ΔCMD có
MA=MC
\(\widehat{AMB}=\widehat{CMD}\)
MB=MD
Do đó: ΔAMB=ΔCMD
b: Xét ΔMAD và ΔMCB có
MA=MC
\(\widehat{AMD}=\widehat{CMB}\)
MD=MB
Do đó: ΔMAD=ΔMCB
=>\(\widehat{MAD}=\widehat{MCB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AD//BC
c: Xét ΔNAK và ΔNBC có
NA=NB
\(\widehat{ANK}=\widehat{BNC}\)(hai góc đối đỉnh)
NK=NC
Do đó; ΔNAK=ΔNBC
=>\(\widehat{NAK}=\widehat{NBC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AK//BC
Ta có: AD//BC
AK//BC
AK,AD có điểm chung là A
Do đó: D,A,K thẳng hàng

a/ Xét △ABM và △DMC có:
\(\begin{matrix}AM=MD\left(gt\right)\\MB=MC\left(gt\right)\\\hat{AMB}=\hat{CMD}\left(đối\text{ }đỉnh\right)\end{matrix}\)
\(\Rightarrow\Delta AMB=\Delta DMC\left(c.g.c\right)\) (đpcm).
b/ Ta có: \(\Delta AMB=\Delta DMC\left(cmt\right)\)
\(\Rightarrow\hat{MAB}=\hat{MDC}\); hai góc ở vị trí so le trong.
Vậy: AB // CD (đpcm).
c/ Xét △BAE có:
\(\begin{matrix}BH\perp AE\left(gt\right)\\AH=HE\left(gt\right)\end{matrix}\)
⇒ BH vừa là đường cao, vừa là đường trung tuyến.
⇒ △BAE cân tại B.
\(\Rightarrow BE=BA\). Mà \(AB=CD\left(\Delta AMB=\Delta DMC\right)\)
Vậy: BE = CD (đpcm).

a: Xét ΔAMB và ΔDMC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔAMB=ΔDMC
b: ta có; ΔAMB=ΔDMC
=>AB=DC
Ta có: ΔAMB=ΔDMC
=>\(\widehat{MAB}=\widehat{MDC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//DC
c: Xét ΔNAB và ΔNCE có
NA=NC
\(\widehat{ANB}=\widehat{CNE}\)(hai góc đối đỉnh)
NB=NE
Do đó: ΔNAB=ΔNCE
=>AB=CE
Ta có: ΔNAB=ΔNCE
=>\(\widehat{NAB}=\widehat{NCE}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CE
Ta có: AB//CE
AB//CD
CE,CD có điểm chung là C
Do đó: E,C,D thẳng hàng
Ta có: EC=AB
CD=AB
Do đó: EC=CD
mà E,C,D thẳng hàng
nên C là trung điểm của ED
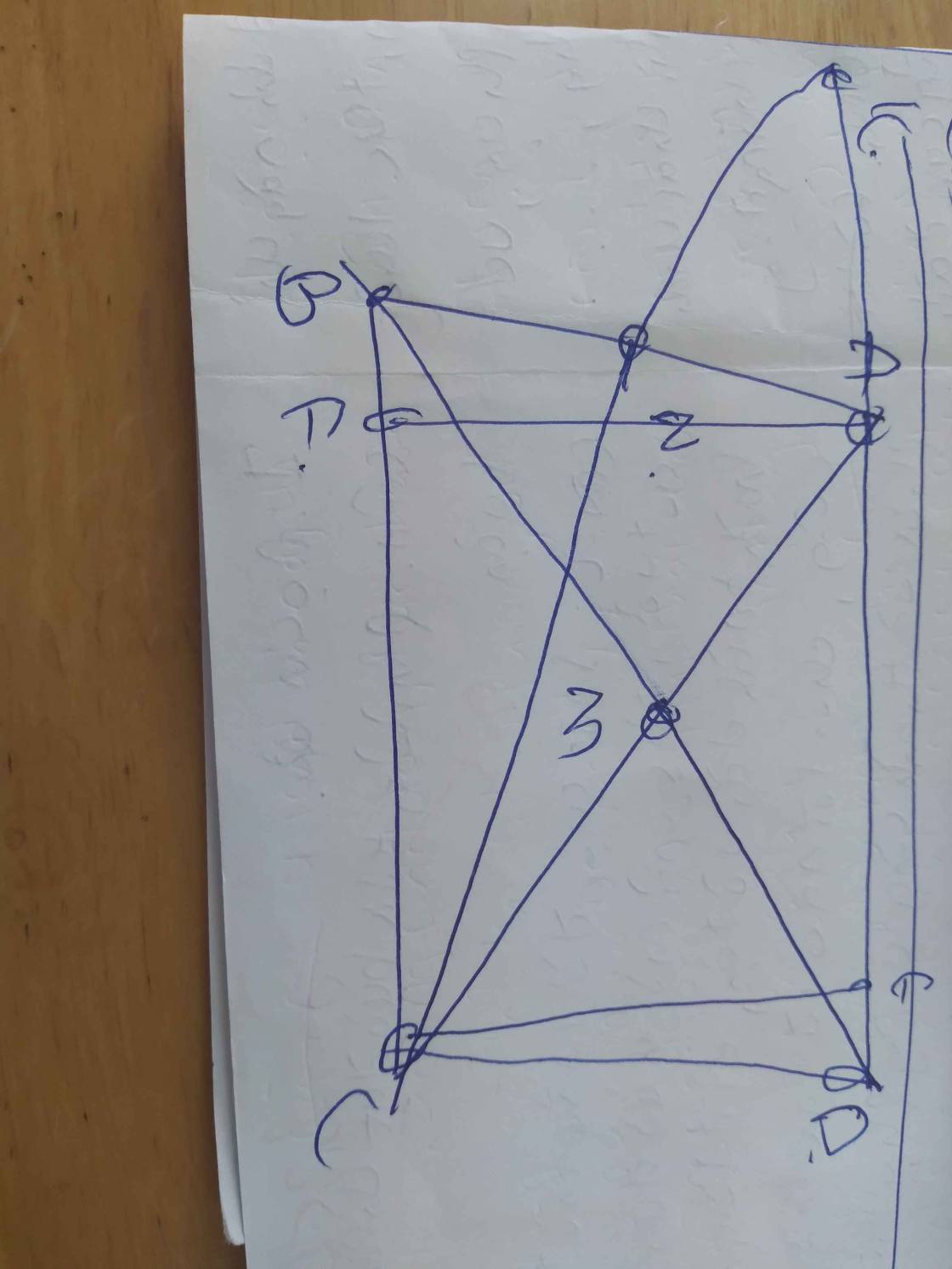


a) xét tam giác AMBvà tam giácCMD có
góc AMB=gócCMD(đối đỉnh)
MA=MC
MD=MB
suy ra tam giác AMB=tam giác CMD
b) tam giác AMB=tam giác CMD(câu a)
AB=CD(hai cạnh tương ứng)
góc DCM=góc MAB(hai góc tương ứng và so le trong)
suy ra AB//CD
câu c đang tìm hiểu từ từ nha tick đi rồi giải câu c luôn cho
a) Xét \(\Delta\)AMB & \(\Delta\)CMD có:
MB=MD( giả thiết)
góc AMB= góc CMD(2 góc đối đỉnh)
AM=MC( vì M là trung điểm của AC)
=>\(\Delta\)AMB=\(\Delta\)CMD(c.g.c)
b) Theo a) \(\Delta\)AMB=\(\Delta\)CMD
=>AB=CD(2 cạnh tương ứng)
=>góc BAM= góc DCM( 2 góc tương ứng)
Mà 2 góc này ở vị trí so le trong=>AB//CD
c) theo b) AB//CD
=> góc ABC= góc BCE( 2 góc so le trong)
Ta có: AB=CD( theo c/m b)
mà CD=CE( vì C là trung điểm DE)
=>AB=EC
Xét \(\Delta\)ABC & \(\Delta\)ECB có:
AB=EC( theo c/m trên)
góc ABC= góc ECB( theo cm trên)
AC là cạnh chung
=>\(\Delta\)ABC=\(\Delta\)ECB(c.g.c)
=>góc ACB= góc EBC( 2 góc tương ứng)
Mà 2 góc này ở vị trí so le trong
=>AC//BE