Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
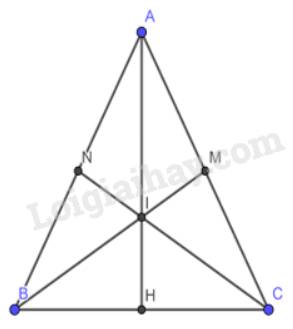
a) Vì tam giác ABC cân tại A theo giả thiết. BM và CN là 2 đường trung tuyến nên M, N là 2 trung điểm của AC, AB.
Vì AB = AC (tính chất tam giác cân)
\( \Rightarrow \dfrac{{AB}}{2} = \dfrac{{AC}}{2} = AN = AM\)
Xét tam giác AMB và tam giác ANC ta có :
AM = AN (cmt)
AB = AC
Góc A chung
\( \Rightarrow \Delta AMB =\Delta ANC\)
\( \Rightarrow BM = CN\) ( 2 cạnh tương ứng )
b) Vì BM và CN là các đường trung tuyến
Mà I là giao điểm của BM và CN
\( \Rightarrow \) I là trọng tâm của tam giác ABC
\( \Rightarrow \) AI là đường trung tuyến của tam giác ABC hay AH đường là trung tuyến của tam giác ABC
\( \Rightarrow \) H là trung điểm của BC

a) Xét △ABM vuông tại A và △DBM vuông tại D có:
BM chung
AB=DB=3cm(gt)
=> △ABM=△DBM (cạnh huyền-cạnh góc vuông) => AM=DM(2 cạnh t/ứ)
b) Xét △AMN và △DMC có:
AMN=DMC(2 góc đối đỉnh)
AM=DM(cmt)
MAN=MDC(gt)
=> △AMN=△DMC(g.c.g) => MN=MC(2 cạnh tướng ứng) => △MCN cân tại M
c) Vì △AMN=△DMC(cmt) => AN=DC(2 cạnh tương ứng)
Ta có AB=BD;AN=DC;BN=AN+AB;BC=BD+DC => BN=BC=> △BNC cân tại B
Vì △ABM=△DBM(cmt)=> ABM=DBM=> NBK=CBK (A thuộc BN; D thuộc BC;M thuộc BK) => BK là phân giác NBC
=> Trong △BNC cân tại B, BK là đường phân giác, đường trung trực, đường trung tuyến, đường cao,... (t/c) => BK là đường trung trực của CN
d) Áp dụng định lý Pytago vào △ABC vuông tại A có: AB2+AC2=BC^2
=> 9+16=25=BC^2 (cm) => BC = 5 cm
Ta có BD+DC=BC;BD=3cm=> DC=2cm
Ta có AN=DC(cmt) => AN=2cm
Áp dụng định lý Pytago vào △ANC vuông tại A có:
AN^2+AC^2=NC^2
=> 4+16=NC^2
=> NC= căn 20 = 2 x căn 5 (cm)
Vì BK là trung trực NC => K là trung điểm NC => KC = 1/2 NC = căn 5 (cm)
Áp dụng định lý Pytago vào △BKC vuông tại K có:
BC^2=BK^2+KC^2 => BK^2=BC^2+KC^2=25-5=20cm => BK=căn 20=2 nhânnhân căn 5 (cm)

a, vì AB=AC(gt) mà D là trung điểm của AB,E là trung điểm AC
=>AD=AE
=>t.giác ADE cân tại A
b,đề sai hay sao ấy

a: Xét ΔBEC và ΔCDB có
BE=CD
\(\widehat{EBC}=\widehat{DCB}\)
BC chung
Do đó: ΔBEC=ΔCDB
Suy ra: CE=DB
b: Xét ΔGBC có \(\widehat{GCB}=\widehat{GBC}\)
nên ΔGBC cân tại G
=>GB=GC
Ta có: GB+GD=BD
GE+GC=CE
mà BD=CE
và GB=GC
nên GD=GE
hay ΔGDE cân tại G
c: Ta có: AB=AC
nên A nằm trên đường trung trực của BC(1)
Ta có: GB=GC
nên G nằm trên đường trung trực của BC(2)
Ta có: MB=MC
nên M nằm trên đường trung trực của BC(3)
Từ (1), (2) và (3) suy ra A,G,M thẳng hàng
Bạn viết lại đề bài đi mik đọc không hiểu