Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
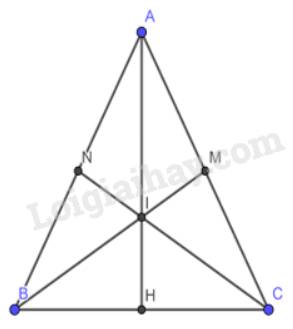
a) Vì tam giác ABC cân tại A theo giả thiết. BM và CN là 2 đường trung tuyến nên M, N là 2 trung điểm của AC, AB.
Vì AB = AC (tính chất tam giác cân)
\( \Rightarrow \dfrac{{AB}}{2} = \dfrac{{AC}}{2} = AN = AM\)
Xét tam giác AMB và tam giác ANC ta có :
AM = AN (cmt)
AB = AC
Góc A chung
\( \Rightarrow \Delta AMB =\Delta ANC\)
\( \Rightarrow BM = CN\) ( 2 cạnh tương ứng )
b) Vì BM và CN là các đường trung tuyến
Mà I là giao điểm của BM và CN
\( \Rightarrow \) I là trọng tâm của tam giác ABC
\( \Rightarrow \) AI là đường trung tuyến của tam giác ABC hay AH đường là trung tuyến của tam giác ABC
\( \Rightarrow \) H là trung điểm của BC

a) Ta thấy \(\widehat{ECN}=\widehat{ACB}\) (Hai góc đối đỉnh)
Tam giác ABC cân tại A nên \(\widehat{ACB}=\widehat{ABC}\Rightarrow\widehat{ECN}=\widehat{DBM}\)
Xét tam giác vuông BDM và CEN có:
BD = CE
\(\widehat{ECN}=\widehat{DBM}\) (cmt)
\(\Rightarrow\Delta BDM=\Delta CEN\) (Cạnh góc vuông và góc nhọn kề)
\(\Rightarrow BM=CN\) (Hai cạnh tương ứng)
b) Do \(\Delta BDM=\Delta CEN\Rightarrow MD=NE\)
Ta thấy MD và NE cùng vuông góc BC nên MD // NE
Suy ra \(\widehat{DMI}=\widehat{ENI}\) (Hai góc so le trong)
Xét tam giác vuông MDI và NEI có:
MD = NE
\(\widehat{DMI}=\widehat{ENI}\)
\(\Rightarrow\Delta MDI=\Delta NEI\) (Cạnh góc vuông và góc nhọn kề)
\(\Rightarrow MI=NI\)
Xét tam giác KMN có KI là đường cao đồng thời trung tuyến nên KMN là tam giác cân tại K.
c) Ta có ngay \(\Delta ABK=\Delta ACK\left(c-g-c\right)\Rightarrow\widehat{ABK}=\widehat{ACK}\) (1) và BK = CK
Xét tam giác BMK và CNK có:
BM = CN (cma)
MK = NK (cmb)
BK = CK (cmt)
\(\Rightarrow\Delta BMK=\Delta CNK\left(c-g-c\right)\Rightarrow\widehat{MBK}=\widehat{NCK}\) (2)
Từ (1) và (2) suy ra \(\widehat{ACK}=\widehat{NCK}\)
Chúng lại là hai góc kề bù nên \(\widehat{ACK}=\widehat{NCK}=90^o\)
Vậy \(KC\perp AN\)

a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
góc BAD chung
Do đó: ΔABD=ΔACE
Suy ra: AD=AE
b: \(BD=\sqrt{10^2-6^2}=8\left(cm\right)\)
d: Xét ΔHBC có \(\widehat{HBC}=\widehat{HCB}\)
nên ΔHBC cân tại H
=>HB=HC
hay H nằm trên đường trung trực của BC(1)
Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường trung trực của BC(2)
Từ (1) và (2) suy ra A,H,M thẳng hàng

a: XétΔABC có
AD là đường cao
BE là đường cao
AD cắt BE tại H
Do đó: CH⊥AB
b: Ta có: ΔFBC vuông tại F
mà FD là trung tuyến
nên FD=BC/2(1)
Ta có: ΔEBC vuông tại E
mà ED là trung tuyến
nên ED=BC/2(2)
Từ (1) và (2) suy ra FD=ED(3)
Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
AB=AC
góc A chung
Do đó: ΔAEB=ΔAFC
SUy ra: AE=AF(4)
Từ (3) và (4) suy ra AD là đường trung trực của EF

a)
*AMN cân
Vì t/g ABC cân tại A (gt)
=>^B=^C
Do đó: ^ABM=^ACN
Xét t/ABM và t/gACN có
góc ^A chung
AB=AC ( vì t/g ABC cân)
^ABM=^ACN (cmt)
Nên t/gABM=t/gACN (g.c.g)
=>AM=AN (2 cạnh tương ứng = nhau)
=> tam giác ANM cân
*MN//BC
Từ tam giác ANM cân nên => ^A+^ANM+^AMN=180o
tam giác ABC cân nên=>^A+^B+^C=180o
Mà ^B=^C
^ANM=^AM
Nên: ^C=^ANM
=>^MCN=^ANM
Mà 2 góc này lại ở vị trí so le trong
Do đó MN//BC (đpcm)
b)
Vì t/g ABC cân tại A
^ABC=^ACB
Mà BM là tia p/g của ^ABC
CN là tia p/g của ^ACB
do đó: ^MBC=^NCB
=> tam giác EBC cân tại E
Xét t/g AEB và t/g AEC có:
AB=AC (vì t/g ABC cân)
^ABM=^ACN (cmt)
=BE=CE (EBC cân)
=> t/gAEB=t/gAEC(c.g.c)
=>^BAE=^CAE (2 góc tương ứng = nhau)
Do đó AE là tia phân giác của t/gBAC (1)
Xét t/g AIB và t/gAIC có
AB=AC ( vì t/g ABC cân)
IB=IC (I là trung điểm BC)
=>tam giác AIB=t/gAIC (c.g.c)
=>^IAB=^IAC (2 góc tương ứng = nhau)
Do đó:AI là tia phân giác của ^BAC (2)
Từ (1) và (2) => A,I,E thằng hàng ( 2 tia phân giác của 1 góc thì thẳng hàng).

a, vì AB=AC(gt) mà D là trung điểm của AB,E là trung điểm AC
=>AD=AE
=>t.giác ADE cân tại A
b,đề sai hay sao ấy