Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
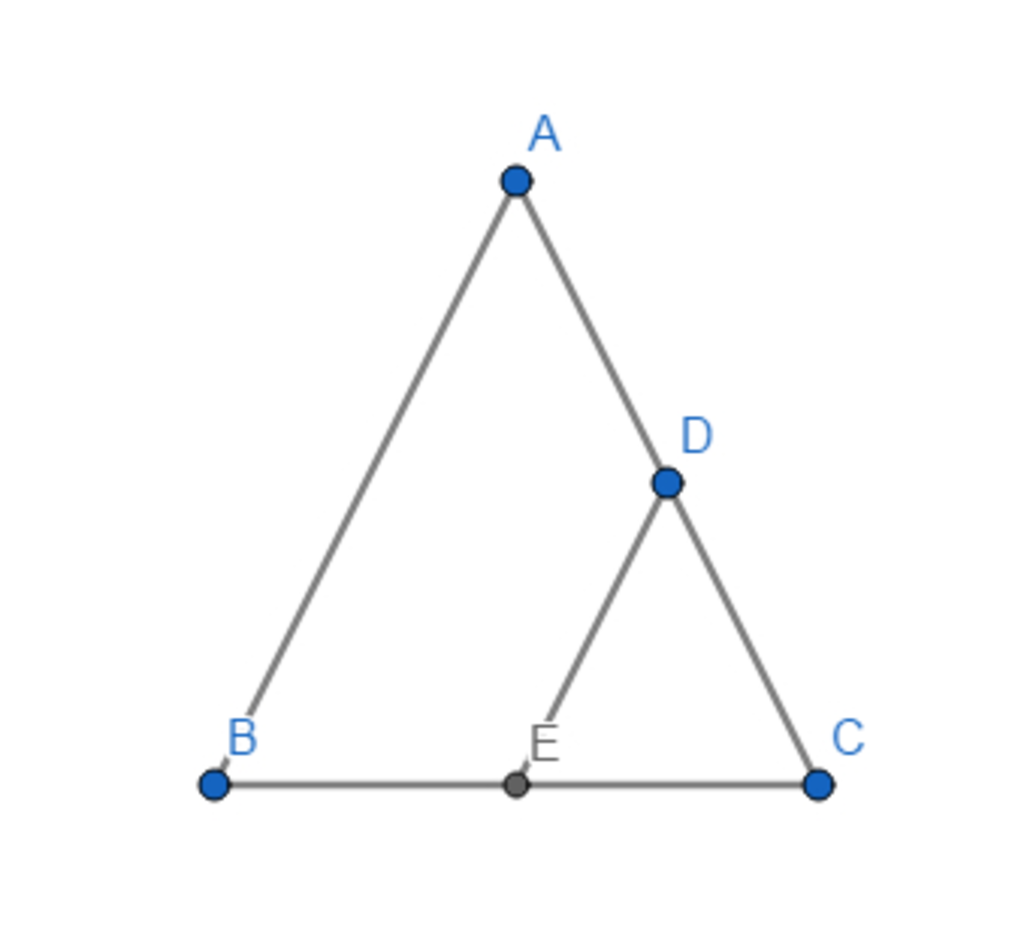
DE // AB (gt).
=> Góc B = Góc DEC (2 góc ở vị trí đồng vị).
Mà Góc B = Góc C (Tam giác ABC cân tại A).
=> Góc DEC = Góc C.
=> Tam DEC là tam giác cân tại D.

a: Ta có: ΔABC cân tại A
mà AD là đường cao
nên D là trung điểm của BC
hay DB=DC
c: Xét ΔKDC có \(\widehat{KDC}=\widehat{KCD}\left(=\widehat{B}\right)\)
nên ΔKDC cân tại K

Lời giải:
Trên tia đối của $DE$ lấy $K$ sao cho \(DK=BC\)
Xét tam giác $KDB$ và $CBD$ có:
\(\widehat{KDB}=\widehat{CBD}\) (so le trong)
\(KD=CB\)
$BD$ chung
Do đó \(\triangle KDB=\triangle CBD(c.g.c)\Rightarrow KB=CD(1)\)
\(DE\parallel BC\) nên theo định lý Ta-let: \(\frac{DB}{EC}=\frac{AB}{AC}=1\) (do ABC cân)
\(\Rightarrow DB=EC\)
Xét tam giac $DBC$ và $ECB$ có:
\(BC\) chung
\(\widehat{DBC}=\widehat{ECB}\)
\(DB=EC\)
\(\Rightarrow \triangle DBC=\triangle ECB(c.g.c)\Rightarrow DC=EB(2)\)
Từ \((1);(2)\Rightarrow 2BE=BE+CD=BE+KB> KE\) theo BĐT tam giác
\(\Rightarrow 2BE> KD+DE\Rightarrow 2BE> BC+DE\Rightarrow BE> \frac{1}{2}(DE+BC)\)
Ta có đpcm.