Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ΔOBC cân tại O ⇒ OB = OC.
ΔAOB và ΔAOC có: AO chung, AB = AC (giả thiết), OB = OC (cmt)
⇒ ΔAOB = ΔAOC (c.c.c).
⇒ ∠BAO = ∠CAO
⇒ AO là tia phân giác của góc BAC
⇒ O cách đều hai cạnh AB, AC

a) Ta có:
AM + MB = AB
AN + NC = AC
Mà AB = AC(△ABC cân) và AM = AN (gt)
=> MB = NC
Xét △MBC và △NCB có:
MB = NC (cmt)
MBC = NCB (△ABC cân)
BC: chung
=> △MBC = △NCB (c.g.c)
=> BN = CM (2 cạnh tương ứng)
b) Vì △MBC = △NCB
=> MCB = NBC (2 góc tương ứng)
=> △BOC cân
c) Vì AM = AN (gt)
=> △AMN cân tại A
=> AMN = \(\frac{180^o-A}{2}\)(1)
Vì △ABC cân tại A
=> ABC = \(\frac{180^o-A}{2}\)(2)
Từ (1) và (2) => AMN = ABC
Mà hai góc AMN và ABC ở vị trí đồng vị
=> MN // BC

tam giác ABC cân tai A. Đường thẳng qua B song song với AC và dường thẳng qua C song song với AC cắt nhau tại D. Trên cạnh AB, AC lần lượt láy các điểm M, N sao cho AM + AN = AB.
= > tam giác DMN đều.

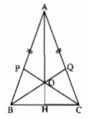
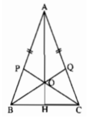
a: Xét ΔPBC và ΔQCB có
PB=QC
\(\widehat{PBC}=\widehat{QCB}\)
BC chung
Do đo: ΔPBC=ΔQCB
Suy ra: \(\widehat{OBC}=\widehat{OCB}\)
hay ΔOBC cân tại O
b: OB=OC
AB=AC
Do đó: AO là đường trung trực của BC
Ta có: ΔABC cân tại A
mà AO là đường trung trực
nên AO là đường phân giác
hay O cách đều hai cạnh AB và AC

Xét tam giác ABN và ACM có: AB = AC (vì tam giác ABC cân tại A); góc A chung; AN = AM (gt)
=> tam giác ABN = ACM (c - g - c)
=> góc ABN = ACM (2 góc tương ứng)
Mà có góc ABC = ACB (do tam giác ABC cân tại A)
Nên góc ABC - ABN = ACB - ACM => góc IBC = ICB => tam giác BIC cân tại I

Bài 1 :
Xét \(\Delta ABC\)có AB = AC (gt)
=> \(\Delta ABC\)cân tại A
=> \(\widehat{B}=\widehat{C}\)
MÀ \(\widehat{C}=\)70
=> \(\widehat{B}=\)70
Xét \(\Delta ABC\)có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
=> \(\widehat{A}+70^0+70^o=180^o\)
=> \(\widehat{A}=180^0-140^o=40^0\)
Vậy \(\widehat{A}=40^0;\widehat{B}=70^0\)

Ta sẽ chứng minh ΔOBC có hai góc OBC và OCB bằng nhau
ΔABQ và ΔACP có: AB = AC, AQ = AP, ∠A chung
⇒ ΔABQ = ΔACP (c.g.c)
⇒ ∠ABQ = ∠ACP.
Mà ∠ABC = ∠ACB (Vì tam giác ABC cân tại A)
⇒ ∠ABC - ∠ABQ = ∠ACB - ∠ACP hay ∠OBC = ∠OCB
⇒ ΔOBC cân tại O.

a) Ta có: \(AM=MB=\dfrac{AB}{2}\)(M là trung điểm của AB)
\(AN=NC=\dfrac{AC}{2}\)(N là trung điểm của AC)
mà AB=AC(ΔABC cân tại A)
nên AM=MB=AN=NC
Xét ΔANB và ΔAMC có
AN=AM(cmt)
\(\widehat{BAN}\) chung
AB=AC(ΔABC cân tại A)
Do đó: ΔABN=ΔACM(c-g-c)
Suy ra: \(\widehat{ABN}=\widehat{ACM}\)(hai góc tương ứng)
hay \(\widehat{MBG}=\widehat{NCG}\)(3)
Xét ΔMBG có \(\widehat{MBG}+\widehat{MGB}+\widehat{BMG}=180^0\)(Định lí tổng ba góc trong một tam giác)(1)
Xét ΔNCG có \(\widehat{NCG}+\widehat{NGC}+\widehat{GNC}=180^0\)(Định lí tổng ba góc trong một tam giác)(2)
Từ (1), (2) và (3) suy ra \(\widehat{MGB}+\widehat{BMG}=\widehat{NGC}+\widehat{CNG}\)
mà \(\widehat{MGB}=\widehat{NGC}\)(hai góc đối đỉnh)
nên \(\widehat{BMG}=\widehat{CNG}\)
Xét ΔBMG và ΔCNG có
\(\widehat{BMG}=\widehat{CNG}\)(cmt)
BM=CN(cmt)
\(\widehat{MBG}=\widehat{NCG}\)(cmt)
Do đó: ΔBMG=ΔCNG(g-c-g)
Suy ra: GM=GN(Hai cạnh tương ứng)