Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔABE và ΔACD có
AB=AC
góc A chung
AE=AD
Do đó: ΔABE=ΔACD
=>BE=CD
Cho tam giác ABC cân tại A lấy các điểm Du và E theo thứ tự AB ,AC sao cho AD=AE . Chứng minh BE= CD

Xét ΔABE và ΔACD có
AB=AC
góc A chung
AE=AD
Do đó: ΔABE=ΔACD
=>BE=CD

tham khảo
https://hoc24.vn/hoi-dap/tim-kiem?id=561093&q=Cho%20tam%20gi%C3%A1c%20ABC%20c%C3%A2n%20t%E1%BA%A1i%20A%20.%20%C4%90i%E1%BB%83m%20D%20thu%E1%BB%99c%20c%E1%BA%A1nh%20AB%20%2C%20%C4%91i%E1%BB%83m%20E%20thu%E1%BB%99c%20c%E1%BA%A1nh%20AC%20sao%20cho%20AD%20%3D%20AE%20.%20G%E1%BB%8Di%20K%20l%C3%A0%20giao%20%C4%91i%E1%BB%83m%20c%E1%BB%A7a%20BE%20v%C3%A0%20CD%20.%20Ch%E1%BB%A9ng%20minh%20r%E1%BA%B7ng%20%20%20a%29%20BE%20%3D%20CD%20%20b%29%20Tam%20gi%C3%A1c%20KBD%20b%E1%BA%B1ng%20tam%20gi%C3%A1c%20KCE%20%20c%29%20AK%20l%C3%A0%20ph%C3%A2n%20gi%C3%A1c%20c%E1%BB%A7a%20g%C3%B3c%20A%20%20d%29%20Tam%20gi%C3%A1c%20KBC%20c%C3%A2n


a: Xét ΔABE và ΔACDcó
AB=AC
góc BAE chung
AE=AD
=>ΔABE=ΔACD
=>BE=CD
b: ΔABE=ΔACD
=>góc ABE=góc ACD
c: góc ABE+góc KBC=góc ABC
góc ACD+góc KCB=góc ACB
mà góc ABE=góc ACD và góc ABC=góc ACB
nên góc KBC=góc KCB
=>KB=KC
d: AB=AC
KB=KC
=>AK là trung trực của BC
=>A,K,I thẳng hàng
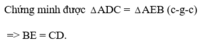
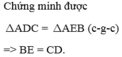

Có: \(\left\{{}\begin{matrix}AD+BD=AB\\AE+EC=AC\end{matrix}\right.\)
Mà: \(\left\{{}\begin{matrix}AD=AE\left(GT\right)\\AB=AC\left(GT\right)\end{matrix}\right.\)
=> BD = EC
Xét ΔBDC và ΔCEB ta có :
BD = EC (cmt)
Góc DBC = Góc ECB (GT)
BC: cạnh chung
=> ΔBDC = ΔCEB (c - g - c)
=> CD = BE (2 cạnh tuwowg ứng)
vậy hình vẽ sao ạ?