
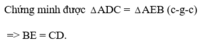
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

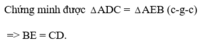

Có: \(\left\{{}\begin{matrix}AD+BD=AB\\AE+EC=AC\end{matrix}\right.\)
Mà: \(\left\{{}\begin{matrix}AD=AE\left(GT\right)\\AB=AC\left(GT\right)\end{matrix}\right.\)
=> BD = EC
Xét ΔBDC và ΔCEB ta có :
BD = EC (cmt)
Góc DBC = Góc ECB (GT)
BC: cạnh chung
=> ΔBDC = ΔCEB (c - g - c)
=> CD = BE (2 cạnh tuwowg ứng)

Bài 2:
Xét ΔADO vuông tại D và ΔAEO vuông tại E có
AO chung
\(\widehat{DAO}=\widehat{EAO}\)
Do đó: ΔADO=ΔAEO
Suy ra: OD=OE
Bài 3:
Xét ΔABE và ΔACD có
AB=AC
\(\widehat{A}\) chung
AE=AD
Do đó: ΔABE=ΔACD
Suy ra: BE=CD

a: XétΔADC và ΔAEB có
AD=AE
góc A chung
AC=AB
=>ΔADC=ΔAEB
b: Xét ΔDBC và ΔECB có
DB=EC
góc DBC=góc ECB
BC chung
=>ΔDCB=ΔEBC
=>góc KBC=góc KCB
=>ΔKBC cân tại K

a: Xét ΔADC và ΔAEB có
AD=AE
góc DAC chung
AC=AB
=>ΔADC=ΔAEB
b: AD+DB=AB
AE+EC=AC
mà AB=AC và AD=AE
nên DB=EC
Xét ΔDBC và ΔECB có
DB=EC
góc DBC=góc ECB
BC chung
=>ΔDBC=ΔECB
=>góc KBC=góc KCB
=>ΔKBC cân tại K