K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

19 tháng 8 2021
b: Xét ΔADB và ΔAEC có
\(\widehat{A}\) chung
\(\widehat{ABD}=\widehat{ACE}\left(=\dfrac{1}{2}\widehat{ABC}\right)\)
Do đó: ΔADB\(\sim\)ΔAEC

KV
11 tháng 9 2023
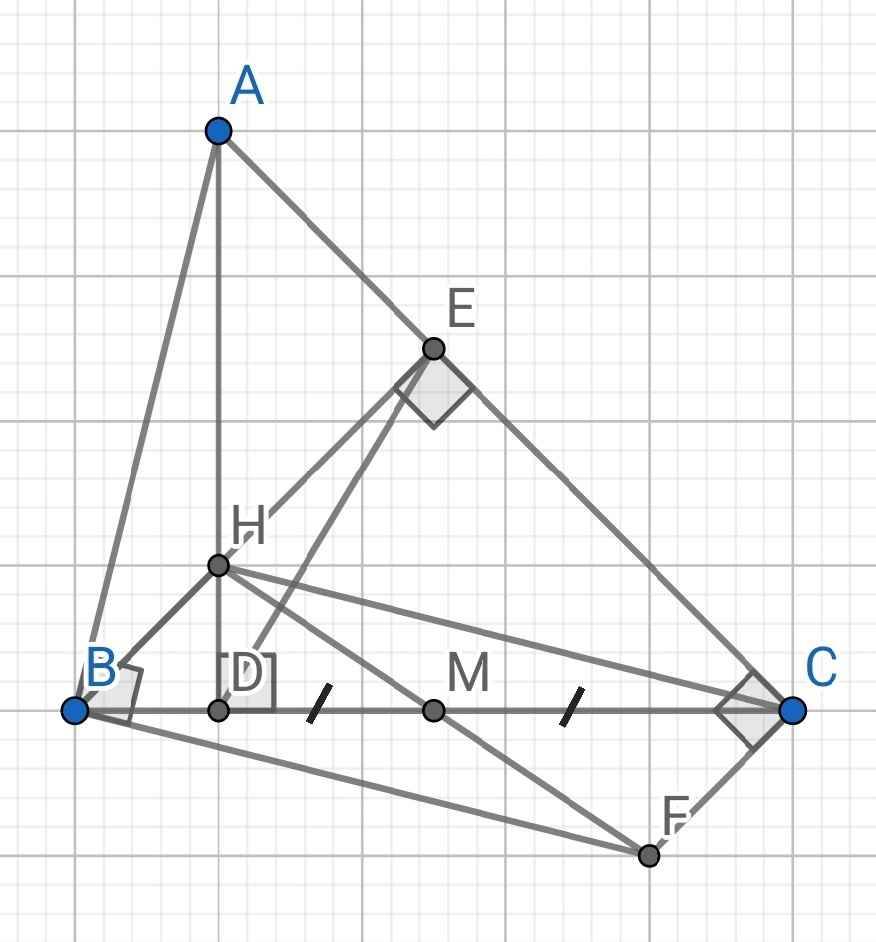 d) Do H là giao điểm của hai đường cao AD và BE của ∆ABC (gt)
d) Do H là giao điểm của hai đường cao AD và BE của ∆ABC (gt)
⇒ CH là đường cao thứ ba của ∆ABC
⇒ CH ⊥ AB
Mà BF ⊥ AB (gt)
⇒ CH // BF
Do CF ⊥ AC (gt)
BE ⊥ AC (gt)
⇒ CF // BE
⇒ CF // BH
Tứ giác BHCF có:
CH // BF (cmt)
CF // BH (cmt)
⇒ BHCF là hình bình hành
e) Do BHCF là hình bình hành (cmt)
Mà M là trung điểm của đường chéo BC (gt)
⇒ M là trung điểm của đường chéo HF
⇒ H, M, F thẳng hàng
a) Xét ΔAHE vuông tại E và ΔABD vuông tại D có
\(\widehat{EAH}\) chung
Do đó: ΔAHE\(\sim\)ΔABD(g-g)
Suy ra: \(\dfrac{AH}{AB}=\dfrac{AE}{AD}\)
hay \(AB\cdot AE=AH\cdot AD\)
b) Xét ΔEHA vuông tại E và ΔEBC vuông tại E có
\(\widehat{AHE}=\widehat{CBE}\)(ΔAHE\(\sim\)ΔABD)
Do đó: ΔEHA\(\sim\)ΔEBC(g-g)
Suy ra: \(\dfrac{EH}{EB}=\dfrac{EA}{EC}\)
hay \(EA\cdot EB=EH\cdot EC\)
d) Ta có: ΔABC cân tại A(gt)
mà AD là đường cao ứng với cạnh đáy BC(Gt)
nên AD là đường trung tuyến ứng với cạnh BC
Suy ra: \(BD=DC=\dfrac{BC}{2}=\dfrac{6}{2}=3\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABD vuông tại D, ta được:
\(AD^2+BD^2=AB^2\)
\(\Leftrightarrow AD^2=5^2-3^2=16\)
hay AD=4(cm)
Xét ΔBEC vuông tại E và ΔBDA vuông tại D có
\(\widehat{B}\) chung
Do đó: ΔBEC\(\sim\)ΔBDA(g-g)
Suy ra: \(\dfrac{BE}{BD}=\dfrac{BC}{BA}\)
\(\Leftrightarrow BE=\dfrac{6\cdot3}{5}=\dfrac{18}{5}=3.6\left(cm\right)\)
Áp dụng định lí Pytago vào ΔBEC vuông tại E, ta được:
\(BC^2=BE^2+EC^2\)
\(\Leftrightarrow EC^2=6^2-3.6^2=23.04\)
hay EC=4,8(cm)