Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBEC vuông tại E và ΔCDB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó: ΔBEC=ΔCDB
b: Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
BD=CE
Do đó: ΔABD=ΔACE
Xét ΔBEK vuông tại E và ΔCDK vuông tại D có
EB=DC
\(\widehat{EBK}=\widehat{DCK}\)
Do đó: ΔBEK=ΔCDK
c: Xét ΔBAK và ΔCAK có
BA=CA
AK chung
BK=CK
Do đó: ΔBAK=ΔCAK
Suy ra: \(\widehat{BAK}=\widehat{CAK}\)
hay AK là tia phân giác của góc BAC

a) Xét \(\Delta\)BCE và \(\Delta\)BCD có:
CEB = BDC (= 90o)
BC: chung
EBC = DCB (\(\Delta\)ABC cân)
\(\Rightarrow\Delta\)BCE = \(\Delta\)BCD (ch-gn)
b) Xét \(\Delta\)BEK và \(\Delta\)CDK có:
BEK = CDK (= 90o)
EB = DC (\(\Delta\)BCE = \(\Delta\)BCD)
EKB = CKD (đối đỉnh)
\(\Rightarrow\Delta\) BEK = \(\Delta\)CDK (cgv-gn)
c) Ta có:
AB = AE + EB
AC = AD + DC
Mà AB = AC (\(\Delta\)ABC cân), EB = DC (\(\Delta\)BCE = \(\Delta\)BCD)
\(\Rightarrow\)AE = AD
Xét \(\Delta\)AKE và \(\Delta\)AKD có:
AEK = ADK (= 90o)
AE = AD (cmt)
AK: chung
\(\Rightarrow\)\(\Delta\) AKE = \(\Delta\)AKD (ch-cgv)
\(\Rightarrow\)KAE = KAD (2 góc tương ứng)
\(\Rightarrow\)AK là phân giác BAC
d) Xét \(\Delta\)AIB và \(\Delta\)AIC có:
AB = AC (\(\Delta\)ABC cân)
AI: chung
IB = IC (I: trung điểm BC)
\(\Rightarrow\)\(\Delta\) AIB = \(\Delta\)AIC (c.c.c)
\(\Rightarrow\)IAB = IAC (2 góc tương ứng)
\(\Rightarrow\)AI là phân giác BAC
Ta có:
+) AK là phân giác BAC
+) AI là phân giác BAC
\(\Rightarrow\)A, K, I thẳng hàng

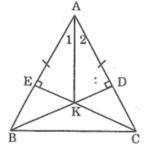
Xét ΔADB vuông tại D và ΔAEC vuông tại E, ta có:
AB = AC (giả thiết)
∠(BAC) chung
⇒ ΔADB = ΔAEC (cạnh huyền, góc nhọn)
⇒ AD = AE (hai cạnh tương ứng)
Xét ΔADK vuông tại D và ΔAEK vuông tại E có:
AD = AE (chứng minh trên)
AK cạnh chung
⇒ ΔADK = ΔAEK (cạnh huyền, cạnh góc vuông)
⇒ ∠(DAK) = ∠(EAK) (hai góc tương ứng)
Vậy AK là tia phân giác của góc BAC.

b,Xét 2 tam giác vuông AEC và ADB có :
AB = AC (gt)
^A : góc chung
=> tam giác AEC =tam giác ADB ( cạnh huyền - góc nhọn)
=> AE = AD ( 2 cạnh tương ứng )
Xét 2 tam giác vuông AEK và ADK có :
AK : cạnh chung
AE = AD ( cmt)
=> tam giác AEK = tam giác ADK ( cạnh huyền - cạnh góc vuông )
=> ^EAK = ^DAK ( 2 góc tương ứng )
=> AK là tia phân giác của góc A

Xét hai tam giác ADB và AEC có:
AB = AC (do \(\Delta ABC\) cân tại A)
\(\widehat{A}\): góc chung
Vậy: \(\Delta ADB=\Delta AEC\left(ch-gn\right)\)
Suy ra: AD = AE (hai cạnh tương ứng)
Xét hai tam giác vuông ADK và AEK có:
AK: cạnh huyền chung
AD = AE (cmt)
Vậy: \(\Delta ADK=\Delta AEK\left(ch-cgv\right)\)
Suy ra: \(\widehat{A_1}=\widehat{A_2}\) (hai góc tương ứng)
Do đó: AK là tia phân giác của góc A.
Giải
Xét tam giác EBC và tam giác DBC có:
E=D=90
B=C(gt)
BC là cạnh chung
=>tam giacs EBC=tam giác DBC( cạnh huyền-góc nhọn)
=>EC=DB( 2 cạnh TƯ)
Xét tam giác AEC và tam giác ADB có;
AB=AC(gt)
EC=BK(cmt)
AK cạnh chung
=> tam giác AEC=tam giác ADB(c.c.c)
=>B1=C1
Xét tam giác ABKvaf tam giác ACK có
AB=AC(gt)
AK chung
B1=C1(cmt)
=>tam giavs ABK=tam giác ACK(c.g.c)
=>A1=A2
=>AK là tia pg của góc A
(cmt: chứng minh trên)
a) Xét tam giác BCE vuông tại E và tam giác CBD vuông tại D:
BC chung.
Góc B = Góc C (Tam giác ABC cân tại A).
=> Tam giác BCE = Tam giác CBD (cạnh huyền - góc nhọn).
b) Xét tam giác ABD vuông tại D và tam giác ACE vuông tại E:
Góc A chung.
AB = AC (Tam giác ABC cân tại A).
=> Tam giác ABD = Tam giác ACE (cạnh huyền - góc nhọn).
=> Góc ABD = Góc ACE (2 góc tương ứng).
Xét tam giác BEK và tam giác CDK:
Góc EBK = Góc DCK (Góc ABD = Góc ACE).
BE = CD (Tam giác BCE = Tam giác CBD).
Góc BEK = Góc CDK (= 90o).
=> Tam giác BEK = Tam giác CDK (g - c - g).
c) Xét tam giác ABC:
BD là đường cao (BD vuông góc với AC).
CE là đường cao (CE vuông góc với AB).
BD cắt CE tại K (gt).
=> K là trực tâm.
=> AK là đường cao.
Xét tam giác ABC cân tại A: AK là đường cao (cmt).
=> AK là đường phân giác góc BAC (Tính chất các đường trong tam giác cân).