Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
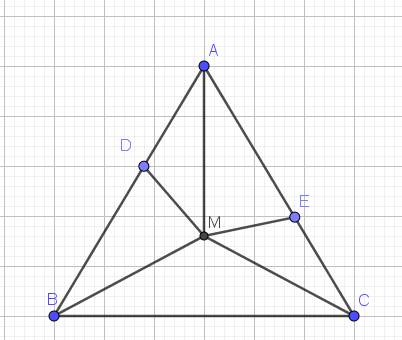
Vì $M$ nằm trên trung trực của $BC$ nên $MB=MC$. $M$ nằm trên đường trung trực của $AB$ nên $MA=MB$
$\Rightarrow MA=MB=MC$
Xét tam giác $AMC$ và $AMB$ có:
$AM$ chung
$AC=AB$ (do $ABC$ là tam giác cân tại $A$)
$MB=MC$
$\Rightarrow \triangle AMC=\triangle AMB$ (c.c.c)
$\Rightarrow \widehat{ACM}=\widehat{ABM}$
Hay $\widehat{ECM}=\widehat{ABM}$
Mà $\widehat{ABM}=\widehat{MAB}$ (do tam giác $MAB$ cân tại $M$ vì $MA=MB$)
$\Rightarrow \widehat{ECM}=\widehat{MAB}=\widehat{DAM}$
Xét tam giác $ECM$ và $DAM$ có:
$EC=DA$ (gt)
$\widehat{ECM}=\widehat{DAM}$ (cmt)
$CM=AM$ (cmt)
$\Rightarrow \triangle ECM=\triangle DAM$ (c.g.c)
$\Rightarrow ME=MD$ (đpcm)

a: Xét ΔBEC và ΔCDB có
BE=CD
\(\widehat{EBC}=\widehat{DCB}\)
BC chung
Do đó: ΔBEC=ΔCDB
Suy ra: CE=DB
b: Xét ΔGBC có \(\widehat{GCB}=\widehat{GBC}\)
nên ΔGBC cân tại G
=>GB=GC
Ta có: GB+GD=BD
GE+GC=CE
mà BD=CE
và GB=GC
nên GD=GE
hay ΔGDE cân tại G
c: Ta có: AB=AC
nên A nằm trên đường trung trực của BC(1)
Ta có: GB=GC
nên G nằm trên đường trung trực của BC(2)
Ta có: MB=MC
nên M nằm trên đường trung trực của BC(3)
Từ (1), (2) và (3) suy ra A,G,M thẳng hàng

a) Vì ΔABCΔ��� cân tại A(gt)�(��)
=> ˆABC=ˆACB���^=���^ (tính chất tam giác cân).
Mà ˆACB=ˆNCE���^=���^ (vì 2 góc đối đỉnh).
=> ˆABC=ˆNCE.���^=���^.
Hay ˆMBD=ˆNCE.���^=���^.
Xét 2 ΔΔ vuông BDM��� và CEN��� có:
ˆBDM=ˆCEN=900(gt)���^=���^=900(��)
BD=CE(gt)��=��(��)
ˆMBD=ˆNCE(cmt)���^=���^(���)
=> ΔBDM=ΔCENΔ���=Δ��� (cạnh góc vuông - góc nhọn kề).
=> DM=EN��=�� (2 cạnh tương ứng).
b) Xét 2 ΔΔ vuông DMI��� và ENI��� có:
ˆMDI=ˆNEI=900(gt)���^=���^=900(��)
DM=EN(cmt)��=��(���)
ˆDIM=ˆEIN���^=���^ (vì 2 góc đối đỉnh)
=> ΔDMI=ΔENIΔ���=Δ��� (cạnh góc vuông - góc nhọn kề).
=> MI=NI��=�� (2 cạnh tương ứng).
=> I là trung điểm của MN.��.
Mà I∈BC(gt)�∈��(��)
=> Đường thẳng BC�� cắt MN�� tại trung điểm I của MN(đpcm).��(đ���).

a: Xét ΔMBD vuông tại D và ΔNCE vuông tại E có
DB=CE
\(\widehat{MBD}=\widehat{NCE}\left(=\widehat{ACB}\right)\)
Do đó: ΔMBD=ΔNCE
Suy ra: DM=EN