Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

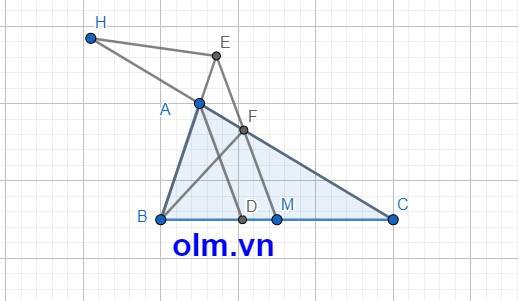
Kéo dài AC về phía A lấy điểm H sao cho CF = FH;
Lúc này bài toán trở thành chứng minh BE = HF
Xét tam giác HBC có: MB = MC (gt); FH = FC
Nên MF là đường trung bình của tam giác HBC ⇒ ME//BH
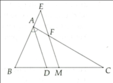
Mặt khác ta có ME//AD ⇒ \(\widehat{AEF}\) = \(\widehat{BAD}\) (hai góc đồng vị) (1)
\(\widehat{BAD}\) = \(\widehat{DAF}\) (AD là phân giác của góc BAC) (2)
\(\widehat{DAF}\) = \(\widehat{AFE}\) (hai góc so le trong) (3)
Kết hợp (1);(2);(3) ta có: \(\widehat{AEF}\) = \(\widehat{AFE}\) ⇒ \(\Delta\)AEF cân tại A ⇒ AE = AF (*)
Vì ME//HB nên: \(\widehat{AHB}\) = \(\widehat{AFE}\) (so le trong)
\(\widehat{ABH}\) = \(\widehat{AEF}\) (so le trong)
⇒ \(\widehat{AHB}\) = \(\widehat{ABH}\) ⇒ \(\Delta\) AHB cân tại A ⇒ AB = AH (**)
Cộng vế với vế của(*) và(*) ta có: AE + AB = AF + AH
⇒ BE = FH
⇒ BE = CF (vì cùng bằng HF)

a: Xét ΔAFH vuông tại F và ΔADB vuông tại D có
góc FAH chung
=>ΔAFH đồng dạng ΔADB
b: góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
=>góc AFE=góc ACB
mà góc FAE chung
nên ΔAFE đồng dạng với ΔACB
góc FEH=góc BAD
góc DEH=góc FCB
mà góc BAD=góc FCB
nên góc FEH=góc DEH
=>EH là phân giác của góc FED