Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

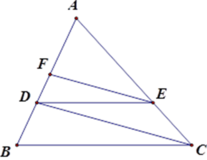
Áp dụng định lý Ta-lét:
Với EF // CD ta có A F A D = A E A C
Với DE // BC ta có A E A C = A D A B
Suy ra A F A D = A D A B , tức là A F 6 = 6 9
Vậy AF = 6.6 9 = 4 cm
Đáp án: C

Bạn ơi bạn kiểm tra lại xem có nhầm chỗ nào không vì:
Nếu EF //AD mà F,D nằm trên AB thì EF và AD có điểm F chung nên không thể //.

a) Áp dụng định lý Thales trong tam giác ABC, ta có:
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\) . Kết hợp với giả thiết ta được \(\dfrac{2}{5}=\dfrac{AE}{7,5}\) \(\Rightarrow AE=3\)
b) Ta thấy \(\dfrac{AE}{AC}=\dfrac{3}{7,5}=\dfrac{2}{5}\) nhưng \(\dfrac{BF}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\ne\dfrac{AE}{AC}\) nên theo định lý Thales đảo, ta không thể có EF//AB.

a: Xét ΔABC và ΔADE có
AB/AD=AC/AE
góc A chung
=>ΔABC đồng dạng với ΔADE
b: ΔBAC đồng dạng với ΔDAE
=>góc ABC=góc ADE
=>BC//DE
c: AE+EC=AC
=>EC=8cm
BE là phân giác góc ABC
=>AB/AE=BC/CE
=>BC/8=9/4
=>BC=18cm
d: DE//BC
=>DE/BC=AE/AC=1/3
=>DE/18=1/3
=>DE=6cm

Xét tứ giác AEDF có
AE//DF
AF//DE
=>AEDF là hình bình hành
=>AD cắt EF tại trung điểm của mỗi đường
=>IE=IF

a: Xét ΔABC có AD/AB=AE/AC
nên DE//BC
=>ΔADE\(\sim\)ΔABC
b: Xét tứ giác BDEF có
BD//EF
DE//BF
Do đó: BDEF là hình bình hành

Bạn thiếu đề