Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật
mà AD là tia phân giác
nên AEDF là hình vuông

a) Xét ΔABC có \(BC^2=AB^2+AC^2\left(5^2=3^2+4^2\right)\)
nên ΔABC vuông tại A(Định lí Pytago đảo)
b) Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔABD=ΔEBD(Cạnh huyền-góc nhọn)
Suy ra: DA=DE(hai cạnh tương ứng)
c) Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE(cmt)
\(\widehat{ADF}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔADF=ΔEDC(Cạnh góc vuông-góc nhọn kề)
Suy ra: DF=DC(Hai cạnh tương ứng)
mà DC>DE(ΔDEC vuông tại E)
nên DF>DE

Xét tứ giác AEDF có
DE//AF
AE//DF
Do đó: AEDF là hình bình hành
mà \(\widehat{DAE}=90^0\)
nên AEDF là hình chữ nhật
mà AD là tia phân giác
nên AEDF là hình vuông

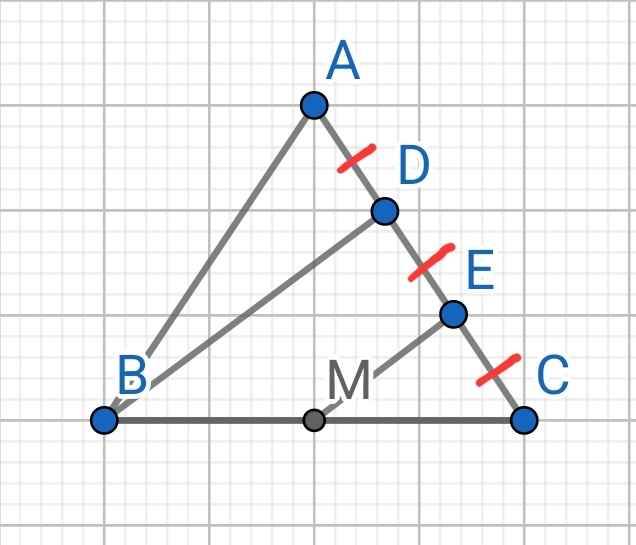
Sửa đề:
AD = DE = EC. BD cắt AM tại I
GIẢI
a) Sửa đề: Chứng mình BDEM là hình thang
Do DE = EC (gt)
⇒ E là trung điểm DC
Mà M là trung điểm BC (gt)
⇒ ME là đường trung bình của ∆BCD
⇒ ME // BD
Tứ giác BDEM có:
ME // BD (cmt)
⇒ BDEM là hình thang
b) Do AD = DE (gt)
⇒ D là trung điểm của AE
Do BD // ME (cmt)
⇒ BI // ME
Mà D là trung điểm của AE (cmt)
⇒ I là trung điểm của AM
⇒ IA = IM

a) Áp dụng định lý Thales trong tam giác ABC, ta có:
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\) . Kết hợp với giả thiết ta được \(\dfrac{2}{5}=\dfrac{AE}{7,5}\) \(\Rightarrow AE=3\)
b) Ta thấy \(\dfrac{AE}{AC}=\dfrac{3}{7,5}=\dfrac{2}{5}\) nhưng \(\dfrac{BF}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\ne\dfrac{AE}{AC}\) nên theo định lý Thales đảo, ta không thể có EF//AB.

Xét tứ giác AEDF có
AE//DF
AF//DE
=>AEDF là hình bình hành
=>AD cắt EF tại trung điểm của mỗi đường
=>IE=IF