
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Vì $\frac{AB}{AC}=\frac{3}{4}$ nên đặt $AB=3a; AC=4a$ với $a>0$
Áp dụng hệ thức lượng trong tam giác vuông:
$\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{1}{AH^2}$
$\frac{1}{(3a)^2}+\frac{1}{(4a)^2}=\frac{1}{81}$
$\frac{25}{144a^2}=\frac{1}{81}$
$a=3,75$ (cm)
Do đó:
$AB=3a=11,25$ (cm)
$AC=4a=15$ (cm)
$BC=\frac{AB.AC}{AH}=\frac{11,25.15}{9}=18,75$ (cm)
Áp dụng định lý Pitago:
$BH=\sqrt{AB^2-AH^2}=\sqrt{11,25^2-9^2}=6,75$ (cm)
$CH=BC-BH=18,75-6,75=12$ (cm)

Áp dụng định lí Pi-ta-go vào tam giác vuông ABC ta có:
B C 2 = A B 2 + A C 2 = 6 2 + 8 2 = 36 + 64 = 100 (cm)
Suy ra: BC = 100 = 10 (cm)
Ta có: sinC = AB/BC = 6/10 = 0,6
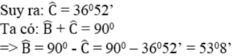

a: AC=căn 5^2+12^2=13cm
sin C=AB/AC=12/13
cos C=5/13
tan C=12/5
cot C=1:12/5=5/12
b: AC=căn 10^2+3^2=căn 109(cm)
sin C=AB/AC=3/căn 109
cos C=BC/AC=10/căn 109
tan C=AB/BC=3/10
cot C=10/3
c: BC=căn 5^2-3^2=4cm
sin C=AB/AC=3/5
cos C=4/5
tan C=3/4
cot C=4/3

a) Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Xét ΔABC vuông tại A có
\(\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{6}{10}=\dfrac{3}{5}\)
nên \(\widehat{C}\simeq37^0\)
\(\Leftrightarrow\widehat{B}=53^0\)

a: ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC^2=6^2+8^2=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot10=6\cdot8=48\)
=>AH=48/10=4,8(cm)
Xét ΔABC vuông tại A có
\(sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\)
nên \(\widehat{C}\simeq37^0\)
ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ABC}=90^0-37^0=53^0\)
b: ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MC=MB=BC/2
Xét ΔMAC có MA=MC
nên ΔMAC cân tại M
=>\(\widehat{MAC}=\widehat{MCA}=\widehat{ACB}\left(1\right)\)
\(\widehat{ACB}+\widehat{ABC}=90^0\)(ΔABC vuông tại A)
\(\widehat{HAB}+\widehat{ABH}=90^0\)(ΔABH vuông tại H)
Do đó: \(\widehat{ACB}=\widehat{HAB}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{MAC}=\widehat{HAB}\)
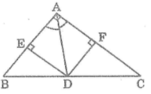
c: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
=>AEHF là hình chữ nhật
=>\(\widehat{AFE}=\widehat{AHE}\)
mà \(\widehat{AHE}=\widehat{ABC}\left(=90^0-\widehat{HAB}\right)\)
nên \(\widehat{AFE}=\widehat{ABC}\)
\(\widehat{AFE}+\widehat{MAC}\)
\(=\widehat{ABC}+\widehat{ACB}=90^0\)
=>FE vuông góc AM tại K
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot CB\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}BH=\dfrac{6^2}{10}=3,6\left(cm\right)\\CH=\dfrac{8^2}{10}=6,4\left(cm\right)\end{matrix}\right.\)
Xét ΔHAB vuông tại H có HE là đường cao
nên \(HA^2=AE\cdot AB\)
=>\(AE\cdot6=4,8^2\)
=>\(AE=3,84\left(cm\right)\)
Xét ΔHAC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\)
=>\(AF=\dfrac{4.8^2}{8}=2,88\left(cm\right)\)
Xét ΔAEF vuông tại A có AK là đường cao
nên \(\dfrac{1}{AK^2}=\dfrac{1}{AE^2}+\dfrac{1}{AF^2}\)
=>\(\dfrac{1}{AK^2}=\dfrac{1}{2,88^2}+\dfrac{1}{3.84^2}\)
=>AK=2,304(cm)