Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a ) Ta có : \(\widehat{A}=\widehat{D}=\widehat{E}=90^o\left(gt\right)\)
\(\Rightarrow ADME\) là hình chữ nhật ( tứ giác có ba góc vuông )
b ) Ta có : ME là đường trung bình của tam giác ABC
\(\Rightarrow ME//AB\) và \(ME=\frac{1}{2}AB=\frac{1}{2}.6=3\left(cm\right)\)
\(\Rightarrow AD=ME=3\left(cm\right)\)( cạnh đối hình chữ nhật )
Lại có : \(\hept{\begin{cases}ME//AB\left(cmt\right)\\MB=MC\left(gt\right)\end{cases}}\)
\(\Rightarrow AE=CE=\frac{AC}{2}=\frac{8}{2}=4\left(cm\right)\)
ADME : hình chữ nhật
\(\Rightarrow A_{ADME}=AD.AE=3.4=12\left(cm^2\right)\)
c ) Dễ thấy AC là đường trung trực của MK
\(\Rightarrow AM=AK\)và \(CM=CK\)
Mà AM = CM \(\left(=\frac{1}{2}BC\right)\) ( \(\Delta ABC\) vuông tại A )
\(\Rightarrow AM=AK=CM=CK\)
\(\Rightarrow AMCK\)là hình thoi ( tứ giác có 4 cạnh bằng nhau )
d ) Ta có : \(ME=\frac{1}{2}AB\)
\(\Rightarrow AB=2ME=MK\)
Hình thoi AMCK là hình vuông \(\Leftrightarrow AC=MK\)
\(\Leftrightarrow AC=AB\) ( vì AB = MK )
\(\Leftrightarrow\Delta ABC\)cân tại A
Mà \(\Delta ABC\) vuông tại A (gt)
Vậy \(\Delta ABC\)vuông cân tại A thì hình thoi AMCK là hình vuông

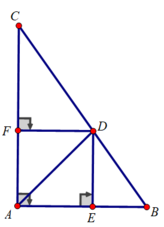
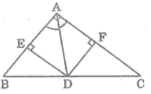
c) Xét tứ giác AEDF có:
∠(EAF) = ∠(AFD) = ∠(AED) = 90 0
⇒ Tứ giác AEDF là hình chữ nhật
Lại có: ΔAFD vuông tại F, có ∠(FAD) = 45 0
⇒ ΔAFD vuông cân tại F
⇒ AF = FD
⇒ tứ giác AEDF là hình vuông
Xét tam giác DEB vuông tại D có:
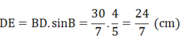
Chu vi hình vuông AEDF là:
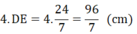
Diện tích hình vuông AEDF là:
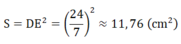

muốn giúp lắm nhưng mới lớp 7 chỉ bt làm phần a,d nghĩ bài a,d là toán lớp 7

a, Aps dụng địnhlí Py-ta-go:
BC^2=AB^2+AC^2=6^2 + 8^2 =100
->BC=10(cm)
b, AD là phân giác góc A:=>BD/CD=AB/AC
=>BD/CD=6/8=3/4
=>BD/3=CD/4
mÀ bD+CD=10->BD/3=CD/4=(BD+CD)/7=10/7
=>bd=10/7*3=30/7(cm)
=>CD=10/7*4=40/7(cm)
c, Ta thấy:
DE vuông góc với AB
DF vg góc với AC =>> Tứ giác AEDF là hình chữ nhật mà AD là p/giac góc A=>Tứ giác AEDF là hình vuông
Góc A: vuông
Ta có: S(ABC)=S(ADB)+S(ADC)
<=>1/2AB*AC=1/2ED*AB+1/2FD*AC
Vì:DE=DF(AEDF là hình vuông)=>DE=DF=(AB*AC)/(AB+AC)=49/14=24/7(cm)
=>S(AEDF)=DE^2=11,8(cm2)
=>C(AEDF)=4DE=4*24/7=13,71(CM


Nên tứ giác AFDE là hình vuông
* Vì DE ⊥ AB, AC ⊥ AB nên DE // AC
Theo định lí Ta-lét ta có: CD/BC = AE/AB

Vì AB^2 + AC^2 = BC^2 ( 6^2 + 8^2 = 10^2 )
=> ΔABC vuông tại A
a. Vì Am là trung tuyến của BC
=> AM =1/2 BC
=> AM = 5cm.
b. Xét tứ giác ADME, ta có:
góc DAE + góc AEM + góc EMD + góc MDA = 360°
=> 90° + 90° + góc EMD + 90° = 360°
=> góc EMD = 90°
=> Tứ giác ADME là hình chữ nhật.