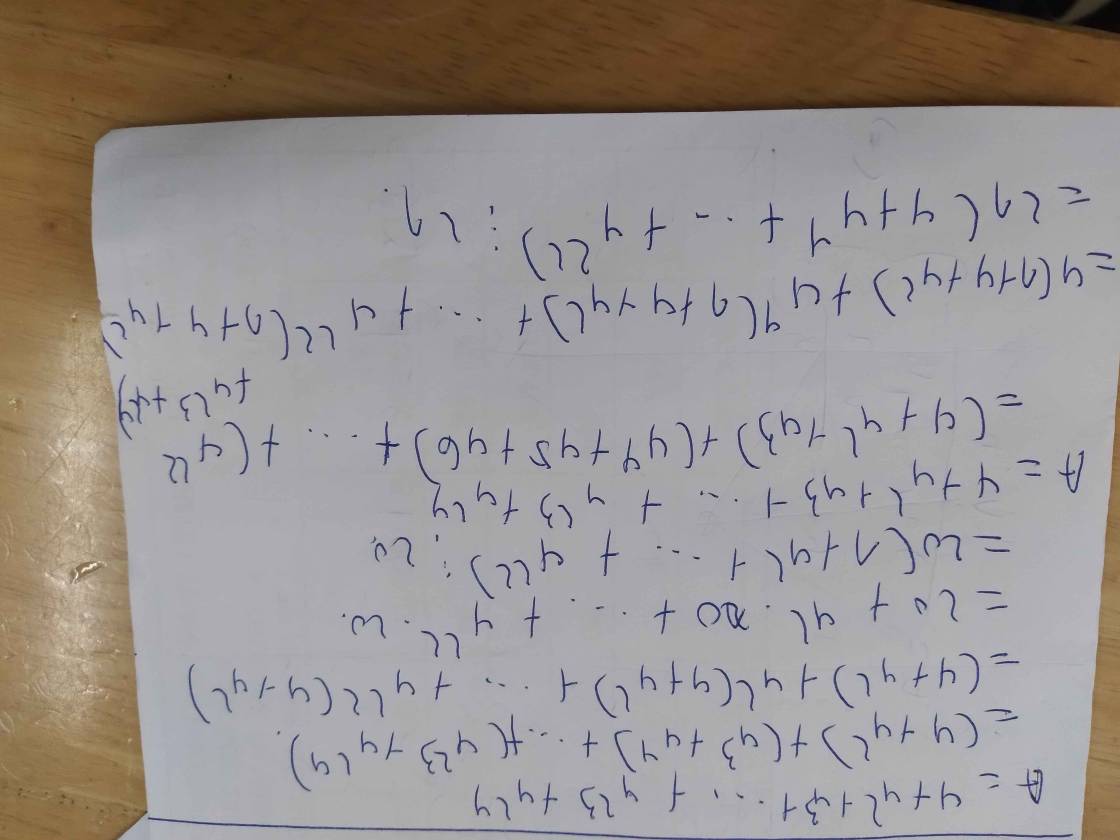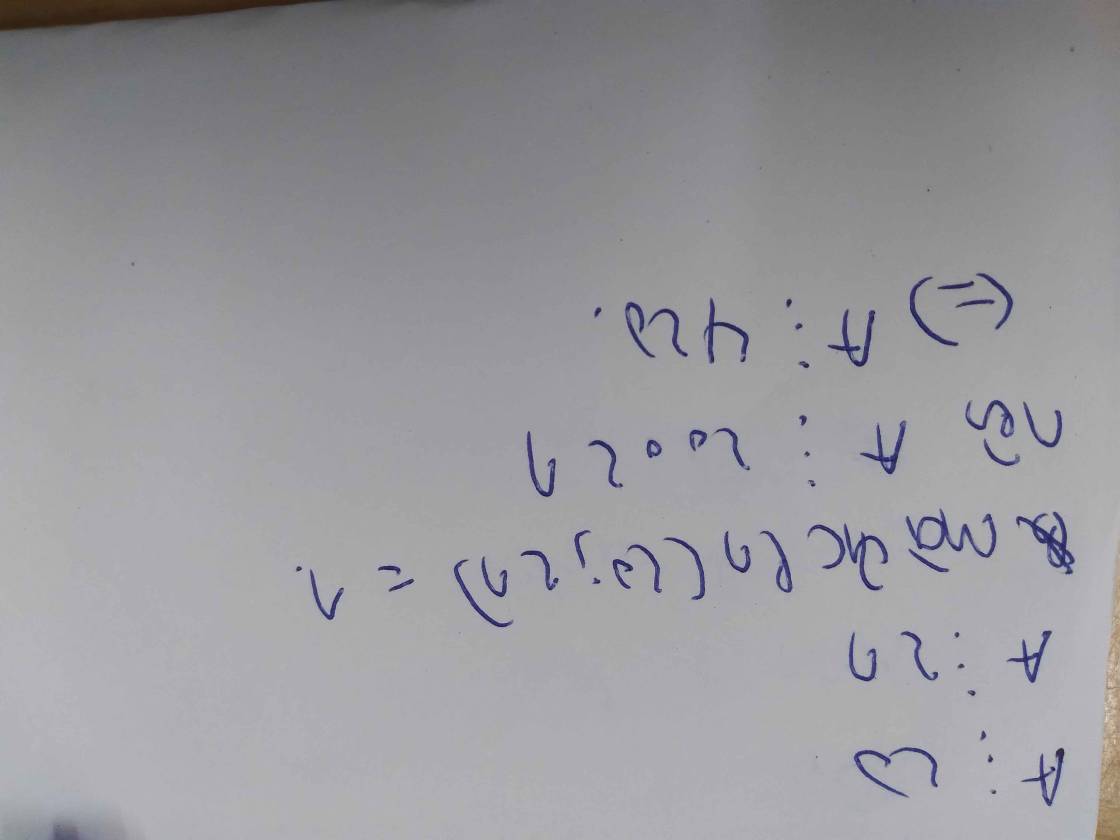Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A = 4 + 4² + 4³ + ... + 4²³ + 4²⁴
Số số hạng của A:
24 - 1 + 1 = 24
Do 24 ⋮ 2 nên ta có thể nhóm các số hạng của A thành từng nhóm mà mỗi nhóm có 2 số hạng như sau:
A = (4 + 4²) + (4³ + 4⁴) + ... + (4²³ + 4²⁴)
= 20 + 4².(4 + 4²) + ... + 4²².(4 + 4²)
= 20 + 4².20 + ... + 4²².20
= 20.(1 + 4² + ... + 4²²) ⋮ 20
Vậy A⋮ 20 (1)
Do 24 ⋮ 3 nên ta có thể nhóm các số hạng của A thành từng nhóm mà mỗi nhóm có 3 số hạng như sau:
A = (4 + 4² + 4³) + (4⁴ + 4⁵ + 4⁶) + ... + (4²² + 4²³ + 4²⁴)
= 4.(1 + 4 + 4²) + 4⁴.(1 + 4 + 4²) + ... + 4²².(1 + 4 + 4²)
= 4.21 + 4⁴.21 + ... + 4²².21
= 21.(4 + 4⁴ + ... + 4²²) ⋮ 21
Vậy A ⋮ 21 (2)
Từ (1) và (2) ⇒ A ⋮ 20 . 21 (do 20 và 21 nguyên tố cùng nhau)
⇒ A ⋮ 420
Vậy A chia hết cho 20; 21; 420

1+7+7 mũ 2+7 mũ 3......+7 mũ 100.Tính a,a là tổng dãy số trên

\(S=2^1+2^2+2^3+2^4+2^5+2^6+..+2^{28}+2^{29}+2^{30}\)
\(S=2.\left(1+2+2^2\right)+2^4.\left(1+2+2^2\right)+...+2^{28}.\left(1+2+2^2\right)\)
\(S=\left(1+2+2^2\right).\left(2+2^4+...+2^{28}\right)\)
\(S=7.\left(2+2^4+...+2^{28}\right)\)
⇒ \(S⋮7\) ( điều phải chứng minh )

\(2^1+2^2+2^3+...+2^{2016}\)
\(=\left(2^1+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{2015}+2^{2016}\right)\)
\(=2\left(1+2\right)+2^3\left(1+2\right)+...+2^{2015}\left(1+2\right)\)
\(=3\left(2+2^3+...+2^{2015}\right)⋮3\)
\(2^1+2^2+2^3+...+2^{2016}\)
\(=\left(2^1+2^2+2^3\right)+\left(2^4+2^5+2^6\right)+...+\left(2^{2014}+2^{2015}+2^{2016}\right)\)
\(=2\left(1+2+2^2\right)+2^4\left(1+2+2^2\right)+...+2^{2014}\left(1+2+2^2\right)\)
\(=7\left(2+2^4+...+2^{2014}\right)⋮7\)

\(S=5+5^2+5^3+...+5^{1992}\)
\(=5\left(1+5\right)+5^3\left(1+5\right)+...+5^{1991}\left(1+5\right)\)
\(=5.6+5^3.6+...+5^{1991}.6=6\left(5+5^3+...+5^{1991}\right)⋮6\)

b: \(B=\left(1+7\right)+7^2\left(1+7\right)+...+7^{100}\left(1+7\right)\)
\(=8\cdot\left(1+7^2+...+7^{100}\right)⋮8\)
c: \(C=4^{39}\left(1+4+4^2\right)=4^{39}\cdot21=4^{38}\cdot84⋮28\)