Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left(x+y+z\right)⋮6\Rightarrow\left(x+y+z\right)⋮2\)
x, y, z không thể đồng thời cả 3 số cùng lẻ ; nghĩa là phải có 1 số chẵn
\(\left\{{}\begin{matrix}\left(x.y.z\right)⋮2\Rightarrow3\left(xyz\right)⋮6\\\left(\left(x-y\right)\left(x+y\right)\left(x+y+z\right)\right)⋮6\end{matrix}\right.\)
\(\Rightarrow A⋮6\Rightarrow dpcm\)

a) \(B=\left(x+y\right)\left(x+z\right)\left(y+z\right)+xyz\)
\(B=\left(x^2+xy+xz+yz\right)\left(y+z\right)+xyz\)
\(B=x^2y+xy^2+xyz+y^2z+x^2z+xyz+xz^2+yz^2+xyz\)
\(B=\left(x^2y+xy^2+xyz\right)+\left(y^2z+yz^2+xyz\right)+\left(x^2z+xz^2+xyz\right)\)
\(B=xy\left(x+y+z\right)+yz\left(x+y+z\right)+xz\left(x+y+z\right)\)
\(B=\left(x+y+z\right)\left(xy+yz+xz\right)\)
b) Ta có:
\(B-3xy=\left(x+y+z\right)\left(xy+yz+xz\right)-3xy\)
Vì x + y + z chia hết cho 6
\(\Rightarrow\left(x+y+z\right)\left(xy+yz+xz\right)\) chia hết cho 6
Vì x + y + z chia hết cho 6
=> Trong 3 số x ; y ; z có ít nhất một số chẵn
\(\Rightarrow3xy\) chia hết cho 6
\(\Rightarrow\left(x+y+z\right)\left(xy+yz+xz\right)-3xy\) chia hết cho 6
\(\Rightarrow B-3xy\) chia hết cho 6
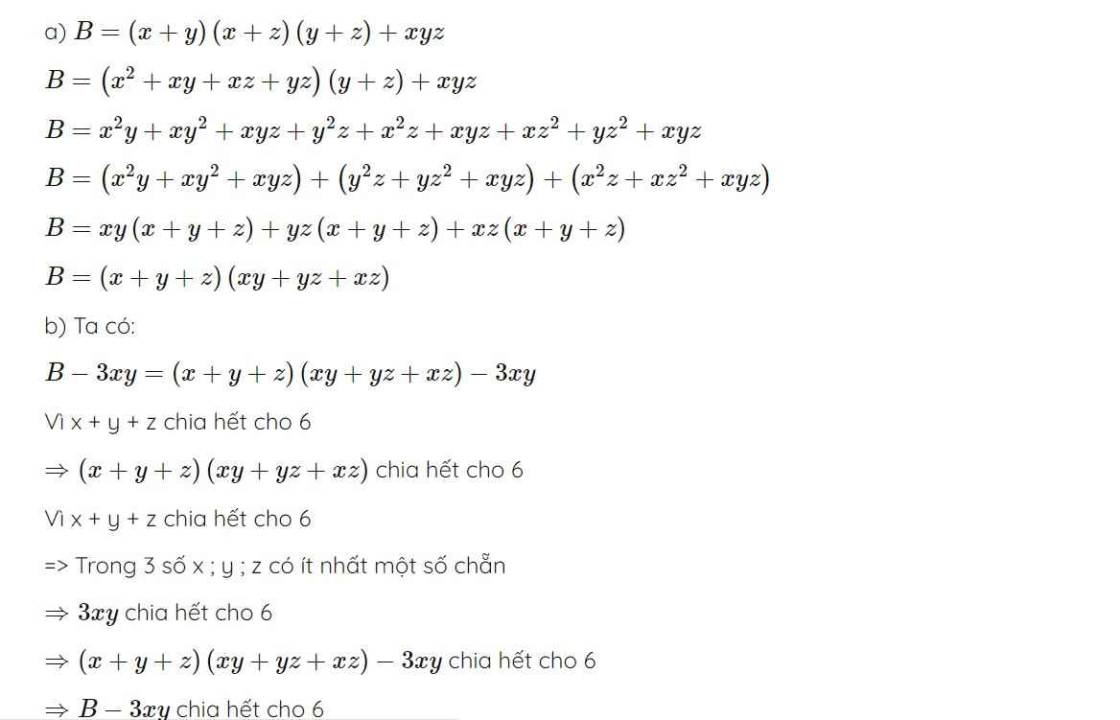
Lời giải:
Biến đổi:
\(P=(x+y)(y+z)(x+z)+xyz=xy(x+y)+yz(y+z)+xz(z+x)+3xyz\)
\(\Leftrightarrow P=(x+y+z)(xy+yz+xz)\)
Với \(x+y+z\vdots 6\Rightarrow P\vdots 6(1)\)
Giả sử \(x,y,z\) đều là các số nguyên lẻ, khi đó \(x+y+z\) lẻ thì không thể chia hết cho $6$ (vô lý)
Do đó , phải tồn tại ít nhất một trong ba số \(x,y,z\) là số chẵn
\(\Rightarrow 3xyz\vdots 6(2)\)
Từ \((1),(2)\Rightarrow Q=P-3xyz\vdots 6\)
Ta có đpcm