Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình mx2 – 4(m – 1) x + 2 = 0
có a = m; b’ = −2(m – 1); c = 2
Suy ra Δ ' = [−2(m – 1)]2 – m.2 = 4m2 – 10m + 4
TH1: m = 0 ta có phương trình 4x + 2 = 0
⇔ x = − 1 2 nên loại m = 0
TH2: m ≠ 0. Để phương trình vô nghiệm thì
a ≠ 0 Δ ' < 0 ⇔ m ≠ 0 4 m 2 − 10 m + 4 < 0
⇔ m ≠ 0 2 m 2 − 5 m + 2 < 0 ⇔ m ≠ 0 2 m 2 − 4 m − m + 2 < 0
⇔ m ≠ 0 2 m ( m − 2 ) − ( m − 2 ) < 0
⇔ m ≠ 0 2 m − 1 m − 2 < 0
⇔ m ≠ 0 2 m − 1 < 0 m − 2 > 0 2 m − 1 > 0 m − 2 < 0 ⇔ m ≠ 0 m < 1 2 m > 2 V L m > 1 2 m < 2
Vậy 1 2 < m < 2 là giá trị cần tìm
Đáp án cần chọn là: C

1) điều kiện của m: m khác 5/2
thế x=2 vào pt1 ta đc:
(2m-5)*4 - 4(m-1)+3=0 <=> 8m-20-4m+4+3=0<=> 4m = 13 <=> m=13/4 (nhận)
lập △'=[-(m-1)]2-*(2m-5)*3 = (m-4)2
vì (m-4)2 ≥ 0 nên phương trình có nghiệm kép => x1= x2 =2
3) vì △'≥0 với mọi m nên phương trình đã cho có nghiệm với mọi m

a. Bạn tự giải
b. Để pt có 2 nghiệm trái dấu
\(\Leftrightarrow ac< 0\Leftrightarrow m+1< 0\Rightarrow m< -1\)
c. Đề bài có vẻ ko chính xác, sửa lại ngoặc sau thành \(x_2\left(1-2x_1\right)...\)
\(\Delta'=\left(m+2\right)^2-4\left(m+1\right)=m^2\ge0\) ; \(\forall m\)
\(\Rightarrow\) Pt đã cho luôn luôn có nghiệm
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m+2\right)\\x_1x_2=m+1\end{matrix}\right.\)
\(x_1\left(1-2x_2\right)+x_2\left(1-2x_1\right)=m^2\)
\(\Leftrightarrow x_1+x_2-4x_1x_2=m^2\)
\(\Leftrightarrow2\left(m+2\right)-4\left(m+1\right)=m^2\)
\(\Leftrightarrow m^2+2m=0\Rightarrow\left[{}\begin{matrix}m=0\\m=-2\end{matrix}\right.\)

Phương trình (m – 3)x2 – 2mx + m − 6 = 0
có a = m – 3; b’ = −m; c = m – 6
Suy ra Δ ' = (−m)2 – (m − 3)(m – 6) = 9m – 18
TH1: m – 3 = 0 ⇔ m = 3 −6x – 3 = 0
⇔ x = − 1 2
TH2: m – 3 ≠ 0 ⇔ m ≠ 3
Để phương trình vô nghiệm thì:
a ≠ 0 Δ ' < 0 ⇔ m ≠ 3 9 m − 18 < 0 ⇔ m ≠ 3 m < 2 ⇔ m < 2
Vậy m < 2 là giá trị cần tìm
Đáp án cần chọn là: B

Trường hợp 1: m=0
Phương trình sẽ là \(-2\cdot\left(0-1\right)x+0-3=0\)
=>2x-3=0
hay x=3/2
=>Phương trình có đúng 1 nghiệm
Trường hợp 2: m<>0
\(\Delta=\left(2m-2\right)^2-4m\left(m-3\right)\)
\(=4m^2-8m+4-4m^2+12m=4m+4\)
a: Để phương trình có nghiệm kép thì 4m+4=0
hay m=-1
c: Để phương trình vô nghiệm thì 4m+4<0
hay m<-1
d: Để phương trình có nghiệm thì 4m+4>=0
hay m>=-1


Phương trình (1) có 4 nghiệm phân biệt khi phương trình (2) có hai nghiệm số dương khi
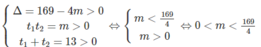

Ta có pt: \(mx^2-3\left(m+1\right)x+m^2-13m-4=0\)
Do pt có nghiệm là x = -2 nên thay vào pt ta có:
\(m\cdot\left(-2\right)^2-3\left(m+1\right)\cdot-2+m^2-13m-4=0\)
\(\Leftrightarrow4m+6\left(m+1\right)+m^2-13m-4=0\)
\(\Leftrightarrow6m+6+m^2-9m-4=0\)
\(\Leftrightarrow m^2-3m+2=0\)
\(\Delta=\left(-3\right)^2-4\cdot1\cdot2=1>0\)
\(\Leftrightarrow\left[{}\begin{matrix}m_1=\dfrac{3+\sqrt{1}}{2}=2\\m_2=\dfrac{3-\sqrt{1}}{2}=1\end{matrix}\right.\)
Nếu m = 1 thì pt là:
\(x^2-3\left(1+1\right)x+1^2-13\cdot1-4=0\)
\(\Leftrightarrow x^2-6x-16=0\)
Theo vi-et: \(x_1+x_2=-\dfrac{-6}{1}\Rightarrow x_2=6-x_2=8\)
Nếu m = 2 thì pt là:
\(2x^2-3\cdot\left(2+1\right)x+2^2-13\cdot2-4=0\)
\(\Leftrightarrow2x^2-9x-26=0\)
Theo vi-et: \(x_1+x_2=-\dfrac{-9}{2}\Leftrightarrow x_2=\dfrac{9}{2}+2=\dfrac{13}{2}\)

Phương trình (1) vô nghiệm khi phương trình (2) có 2 nghiệm số âm hoặc vô nghiệm.
Nếu phương trình (2) có 2 nghiệm âm thì theo hệ thức Vi-ét ta có:
t 1 + t 2 = 13 > 0 vô lý
Vậy phương trình (1) vô nghiệm khi phương trình (2) vô nghiệm.
Suy ra: ∆ = 169 - 4m < 0 ⇔ m > 169/4}