K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 2 2020
\(m^2+m+1=\left(m+\frac{1}{2}\right)^2+\frac{3}{4}\ne0\) \(\forall m\Rightarrow\) phương trình là bậc nhất một ẩn với mọi m
Ta có \(x=\frac{m^2-m+1}{m^2+m+1}=\frac{3\left(m^2+m+1\right)-2m^2-4m-2}{m^2+m+1}=3-\frac{2\left(m+1\right)^2}{m^2+m+1}\le3\)
\(\Rightarrow x_{max}=3\) khi \(m=-1\)
\(x=\frac{3m^2-3m+3}{3\left(m^2+m+1\right)}=\frac{m^2+m+1+2m^2-4m+2}{3\left(m^2+m+1\right)}=\frac{1}{3}+\frac{2\left(m-1\right)^2}{m^2+m+1}\ge\frac{1}{3}\)
\(x_{min}=\frac{1}{3}\) khi \(m=1\)
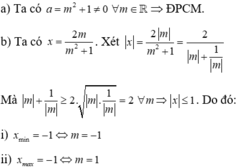


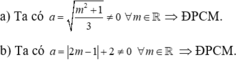

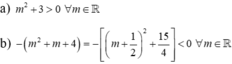
a) m2+1\(\ge\)1 \(\forall\)m, suy ra phương trình đã cho là phương trình bậc nhất một ẩn với mọi m.
b) Nghiệm của phương trình đã cho là x=\(\dfrac{2m}{m^2+1}\) (*).
Áp dụng BĐT Co-si cho hai số dương m2 và 1, ta có:
m2+1\(\ge\)2\(\sqrt{m^2.1}\)=2|m|.
Dấu "=" xảy ra khi và chỉ khi m2=1 \(\Rightarrow\) m=\(\pm\)1.
Với m=1, x=1.
Với m=-1, x=-1.
So sánh hai giá trị của x, ta kết luận: giá trị m cần tìm là m=1.
e cảm ơn ạ