
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

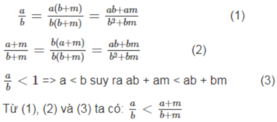

\(\frac{a}{b}\)< 1 <=> a < b <=> a.m < b.m <=> ab + a.m < ab + b.m
<=> a(b + m) < b(a + m)
<=> \(\frac{a}{b}\)< \(\frac{a+m}{b+m}\)

1,\(\frac{a}{b}=\frac{a\left(b+m\right)}{b\left(b+m\right)}=\frac{ab+am}{b^2+bm}\)
2,\(\frac{a+m}{b+m}=\frac{b\left(a+m\right)}{b\left(b+m\right)}=\frac{ab+bm}{b^2+bm}\)
3,\(\frac{a}{b}<1\) =>a<b =>ab+am<ab+bm
Từ 1,2 và 3 ta có :\(\frac{a}{b}<\frac{a+m}{b+m}\)

ta có : x < y hay a/m < b/m => a < b.
So sánh x, y, z ta chuyển chúng cùng mẫu : 2m
x = a/m = 2a/ 2m và y = b/m = 2b/2m và z = (a + b) / 2m
mà : a < b
suy ra : a + a < b + a
hay 2a < a + b
suy ra x < z (1)
mà : a < b
suy ra : a + b < b + b
hay a + b < 2b
suy ra z < y (2)
:D

Câu 1: Giải
\(\frac{a}{b}< 1\Leftrightarrow a< b\)
\(\Leftrightarrow am< bm\)
\(\Leftrightarrow ab+am< ab+bm\)
\(\Leftrightarrow a\left(b+m\right)< b\left(a+m\right)\)
\(\Leftrightarrow\frac{a}{b}< \frac{a+m}{b+m}\left(đpcm\right)\)
Câu 2: Giải
Ta có : \(\hept{\begin{cases}\frac{437}{564}=1-\frac{127}{564}\\\frac{446}{573}=1-\frac{127}{573}\end{cases}}\)
Vì \(\frac{127}{564}>\frac{127}{573}\) nên \(\frac{437}{564}>\frac{446}{573}\)

Ta có x < y ; m > 0
=> \(\frac{a}{m}< \frac{b}{m}\)
=> a < b (vì m > 0)
Lại có x = \(\frac{a}{m}=\frac{2a}{2m}=\frac{a+a}{2m}< \frac{a+b}{2m}=y\)(vì a < b nên a + a < a + b)
=> x < z (1)
Mặt khác \(y=\frac{b}{m}=\frac{2b}{2m}=\frac{b+b}{2m}>\frac{a+b}{2m}=z\)(vì b > a nên b +b > b + a)
=> y > z (2)
Từ (1) và (2) => x < z < y (đpcm)