Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xet tam giac COA can tai O( OA= OC) co CI vua la duong cao vua la trung tuyen ung voi AO nen tam giac OAC deu. Suy ra goc COA bang 60do , suy ra so do cung CA bang 60do. Suy ra goc COB bang 180-60=120 suy ra so do cung CA bang 120. Co: HCA=1/2sd cungCA=60/2=30 (1)
Co goc CHB=1/2(sd cungCB- sd cungCA) =1/2(120-60)=1/2*60=30 (2)
Tu (1); (2) suy ra: tam giac ACH can tai A. Suy ra AC= AH (3)
Lai co: tam giac CAO deu nen CA= CO (4)
Tu (3);(4)suy ra CA=CO=AH⏩ tam giac CHO vuong tai C
➡CO vuong goc voi HC tai C
Vay HC la tiep tuyen
b). Tu giac ACOD la hinh thoi
Tu giac co 4 canh ( CA= CO=OD=DA) bang nhau
c).

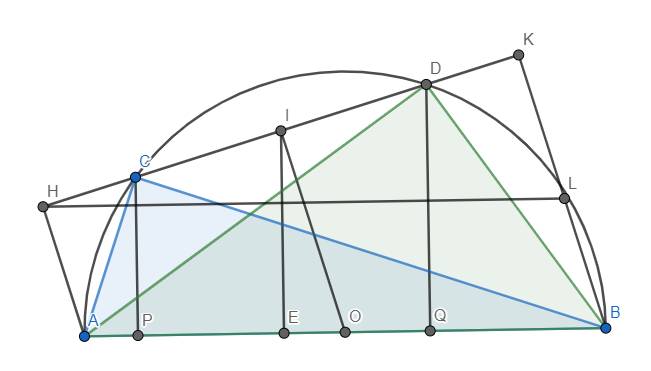
a) Ta thấy OI//AH//BK \(\left(\perp CD\right)\).
Xét hình thang ABKH (AH//BK), O là trung điểm AB. OI//AH \(\left(I\in HK\right)\) nên I là trung điểm HK.
b) Hạ \(CP\perp AB\) tại P, \(DQ\perp AB\) tại Q. Khi đó IE//CP//DQ \(\left(\perp AB\right)\).
Xét hình thang CDQP (CP//DQ) có I là trung điểm CD (hiển nhiên), IE//CP và \(E\in PQ\) nên IE là đường trung bình của hình thang CDQP \(\Rightarrow IE=\dfrac{CP+DQ}{2}\)
Lại có \(S_{ACB}=\dfrac{1}{2}AB.CP\), \(S_{ADB}=\dfrac{1}{2}.AB.DQ\)
\(\Rightarrow S_{ACB}+S_{ADB}=AB.\dfrac{CP+DQ}{2}=AB.IE\) (đpcm)
c) Ta có \(S_{AHKB}=\dfrac{AH+BK}{2}.HK=OI.HK\)
Do dây CD có độ dài không đổi nên khoảng cách từ O đến dây CD là OI cũng không đổi. Như vậy ta chỉ cần tìm vị trí của C để HK lớn nhất.
Thật vậy, dựng hình bình hành ABLH. Khi đó vì BK//AH nên \(L\in BK\). Đồng thời ta luôn có \(HK\le HL=AB\), suy ra \(S_{AHKB}\le OI.AB\).
Dấu "=" xảy ra \(\Leftrightarrow HK=HL\) \(\Leftrightarrow K\equiv L\) \(\Leftrightarrow\) AHKB là hình bình hành \(\Leftrightarrow\) HK//AB hay CD//AB \(\Rightarrow OI\perp AB\). Vậy C là điểm sao cho \(OI\perp AB\).
(Nếu muốn tìm cụ thể vị trí của C, thì mình nói luôn nó là điểm C sao cho \(sđ\stackrel\frown{AC}=180^o-2arc\cos\left(\dfrac{CD}{AB}\right)\) nhé. Chứng minh cái này dễ, mình nhường lại cho bạn.)
Chỗ vị trí C mình sửa lại là \(sđ\stackrel\frown{AC}=90^o-arc\sin\dfrac{CD}{AB}\) nhé.

a/
\(AH^2=HB.HC\) (trong tg vuông bình phương đường cao hạ từ đỉnh góc vuông xuống cạnh huyền bằng tích các hình chiếu của 2 cạnh góc vuông trên cạnh huyền)
\(\Rightarrow AH=\sqrt{HB.HC}=\sqrt{4.9}=6cm\)
\(\tan\widehat{ABC}=\dfrac{AH}{HB}=\dfrac{6}{4}=\dfrac{3}{2}\)
b/
Xét tg vuông AHB có
\(HB^2=BD.AB\) (trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
Xét tg vuông AHC có
\(HC^2=CE.AC\) (lý do như trên)
\(CE.BD.AC.AB=HB^2.HC^2=\left(HB.HC\right)^2\)
Mà \(HB.HC=AH^2\) (cmt)
\(\Rightarrow CE.BD.AC.AB=AH^4\)
c/
\(HD\perp AB;AC\perp AB\) => HD//AC => HD//AE
\(HE\perp AC;AB\perp AC\) => HE//AB => HE//AD
=> ADHE là hình bình hành mà \(\widehat{A}=90^o\) => ADHE là HCN
Xét tg vuông ADH và tg vuông ADE có
HD = AE (cạnh đối HCN)
AD chung
=> tg ADH = tg ADE (Hai tg vuông có 2 cạnh góc vuông = nhau)
\(\Rightarrow\widehat{AED}=\widehat{AHD}\)
\(\widehat{AHD}=\widehat{B}\) (cùng phụ với \(\widehat{BAH}\) )
\(\Rightarrow\widehat{AED}=\widehat{B}\) (1)
\(\widehat{C}+\widehat{B}=90^o\) (2)
\(\widehat{IAE}+\widehat{AED}=90^o\Rightarrow\widehat{IAE}+\widehat{B}=90^o\) (3)
Từ (2) và (3) => \(\widehat{IAE}=\widehat{C}\) => tg AIC cân tại I => IA=IC
Ta có
\(\widehat{IAE}+\widehat{BAI}=\widehat{A}=90^o\)
\(\Rightarrow\widehat{C}+\widehat{BAI}=90^o\) mà \(\widehat{C}+\widehat{B}=90^o\)
\(\Rightarrow\widehat{BAI}=\widehat{B}\) => tg ABI cân tại I => IA=IB
Mà IA= IC (cmt)
=> IB=IC => I là trung điểm của BC

a. Tứ giác ACHD có hai đường chéo cắt nhau tại trung điểm mỗi đường nên nó là hình bình hành. Lại có \(CD\perp AH\) nên đây là hình thoi.
b. Ta thấy \(AC\perp CB;HE\perp CB\) mà DH // AC nên \(DH\perp BC\) hay D, H ,E thẳng hàng. Vậy các hình thang trong hình vẽ trên là: ACDE; ACHD; EHAC.
c. Do tam giác EDC vuông tại E nên IE =ID =IC hay \(\widehat{IEH}=\widehat{IDE}\) . Mà \(\widehat{IDE}=\widehat{CBH}\)(Cùng phụ với \(\widehat{ICB}\) ) nên \(\widehat{IEH}=\widehat{CBH}\)
Lại có tam giác EHB cũng vuông tại E nên KB = KE hay \(\widehat{CBH}=\widehat{BEK}\)
Vậy thì \(\widehat{IEH}=\widehat{BEK}\). Từ đó suy ra \(\widehat{IEK}=\widehat{IEH}+\widehat{HEK}=\widehat{BEK}+\widehat{HEK}=\widehat{HEB}=90^o\)
Vậy \(IE\perp EK\left(đpcm\right)\)