Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nối O với H
Xét đg tròn (O), có:
OK∈ đg kính
K là td của HI (gt)
HI là dây không đi qua tâm
⇒OK⊥HI tại K
⇒HKI=90o
⇒ΔHKI vg tại K
Xét ΔHKI vg tại K, có:
HK2+OK2=OH2(ĐL Pi ta go)
Mà HK=8 cm (K là td của HI)
OH= 10cm (=R)
⇒OK2=36
⇒OK=6 cm (Vì OK>0)

Xét \(\left(O\right)\) có
OM là một phần đường kính
AB là dây
M là trung điểm của AB
Do đó: OM\(\perp\)AB tại M
Ta có: M là trung điểm của AB
nên \(AM=BM=\dfrac{AB}{2}=8cm\)
Áp dụng định lí Pytago vào ΔOMA vuông tại M, ta được:
\(OM^2+MA^2=OA^2\)
\(\Leftrightarrow OM^2=36\)
hay OM=6cm

b: ΔOCD cân tại O
mà OM là đường cao
nên OM là phân giác của góc COD
Xét ΔOCM và ΔODM có
OC=OD
góc COM=góc DOM
OM chung
Do đó: ΔOCM=ΔODM
=>góc ODM=90 độ
=>MD là tiếp tuyến của (O)
c: KD=CD/2=8
OK=căn 10^2-8^2=6
OK*OM=OD^2
=>OM=10^2/6=100/6=50/3

Lời giải:
Tam giác $OAB$ cân tại $O$ (do $OA=OB=R$) nên đường trung tuyến $OH$ đồng thời là đường cao.
$\Rightarrow OH\perp AB$
$AH=\frac{1}{2}AB=8$ (cm)
Áp dụng định lý Pitago cho tam giác vuông $HAO$:
$R=AO=\sqrt{OH^2+AH^2}=\sqrt{6^2+8^2}=10$ (cm)
Đáp án D.

Câu 1:
Gọi giao điểm của OC với AB là H
Vì OC\(\perp\)AB nên OH\(\perp\)AB tại H
=>OH là khoảng cách từ O xuống dây AB
Ta có: ΔOAB cân tại O
mà OH là đường cao
nên H là trung điểm của AB
=>HA=HB=AB/2=8(cm)
ΔOHA vuông tại H
=>\(OH^2+HA^2=OA^2\)
=>\(OH^2=10^2-8^2=36\)
=>\(OH=\sqrt{36}=6\left(cm\right)\)
Câu 2:
a: Xét (O) có
AB là đường kính
BC là dây
Do đó: AB>BC
b: Xét (O) có
ΔCAB nội tiếp
AB là đường kính
Do đó: ΔCAB vuông tại C
c: Xét ΔACB có
O là trung điểm của AB
OM//CB
Do đó: M là trung điểm của AC

Bạn sử dụng tính chất đường kính vuông góc với 1 dây không đi qua tâm thì đi qua trung điểm dây ấy (đọc lại SGK Toán 9 tập 1 trang 103).
b) Theo câu a thì IC=ID=8cmIC=ID=8cm.
Áp dụng định lý Pytago cho tam giác OIC vuông tại I tính được OI=6cmOI=6cm.
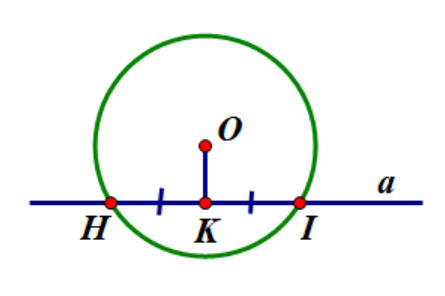
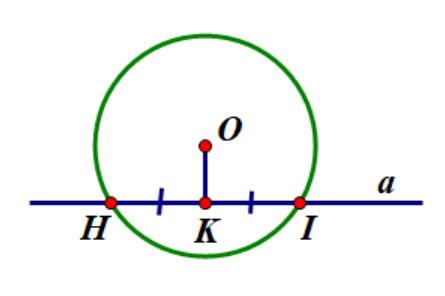 Cho (O;10cm) và dây HI = 16cm. Tính OK = ?
Cho (O;10cm) và dây HI = 16cm. Tính OK = ?