Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, ta có \(\widehat{ADB}\)là góc nội tiếp chắn nửa đường tròn => \(\widehat{ADB}=90^0\)hay \(\widehat{EDB}=90^0\)
Xét tứ giác BDEH có :
\(\widehat{EHB}=90^0\left(CH\perp AB\right)\)
\(\widehat{EDB}=90^0\left(cmt\right)\)
=> tugiac BDEH noi tiep
b,
ta có \(\widehat{ADC}=\widehat{ABC}\)( BDEH noitiep cmt)
mà \(\widehat{ABC}+\widehat{CAB}=90^0\)(góc ACB=90 độ, góc nt chắn nửa đg tròn)
\(\widehat{ACH}+\widehat{CAB}=90^0\)( góc AHC=90 độ vì CH vuông với AB)
=> \(\widehat{ABC}=\widehat{ACH}\)
=> \(\widehat{ACH}=\widehat{ADC}\left(=\widehat{ABC}\right)\)hay góc ADC= góc ACE
Xét tam giác ACE và tam giác ADC
\(\widehat{ADC}=\widehat{ACE}\left(cmt\right)\)
góc CAD chung
=> tam giác ACE đồng dạng với tam giác ADC (g-g)
=> \(\frac{AC}{AD}=\frac{AE}{AC}\)
=> \(AC^2=AD.AE\)(1)
Tam giác ABC vuông tại C có AH là đường cao
=> BC2= BH.BA (hethucluong) (2)
(1);(2) => \(AC^2+BC^2=AE.AD+BH.BA\)
mà AC2+ BC2= AB2 ( pytago trong tam giác ABC vuông ở C)
=> \(AB^2=AE.AD+BH.BA\)

Câu này khó thât đấy nhưng mình giải ra rồi nek
Hình bạn tự vẽ nha
Ta có CH vuông góc AD
Và BD vuông góc AD( góc D nội tiếp chắn nữa đường tròn )
=> CH // BD
=> Góc HCA = Góc DBA ( đồng vị)
Lại có Góc AND = Góc ABD ( cùng chắn cũng AD)
Trong tứ giác AECN có
Góc AND= góc ABD
Vì 2 góc bằng nhau cùng nhìn một cạnh
=> Bốn điểm A,E,N,C thuộc một đường tròn
Hay tứ giác AECN nội tiếp

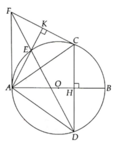
a, Học sinh tự chứng minh
b, DADB vuông tại D, có đường cao DH Þ A D 2 = AH.AB
c, E A C ^ = E D C ^ = 1 2 s đ E C ⏜ ; E A C ^ = K H C ^ (Tứ giác AKCH nội tiếp)
=> E D C ^ = K H C ^ => DF//HK (H là trung điểm DC nên K là trung điểm FC) => Đpcm