Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

B C A x y D E O I J G
a/
\(\widehat{BAC}=90^o\) (góc nt chắn nửa đường tròn) \(\Rightarrow AB\perp AC\Rightarrow AI\perp AC\)
\(OE\perp AC\) (Hai tiếp tuyến cùng xp từ 1 điểm thì đường thẳng nối điểm đó với tâm đường tròn vuông góc với đường thẳng nối hai tiếp điểm) \(\Rightarrow OJ\perp AC\)
=> AI//OJ (cùng vuông góc với AC) (1)
\(\widehat{BAC}=90^o\) (cmt) \(\Rightarrow AC\perp AB\Rightarrow AJ\perp AB\)
\(OD\perp AB\) (Hai tiếp tuyến cùng xp từ 1 điểm thì đường thẳng nối điểm đó với tâm đường tròn vuông góc với đường thẳng nối hai tiếp điểm) \(\Rightarrow OI\perp AB\)
=> AJ//OI (cùng vuông góc với AB) (2)
=> AIOJ là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
\(\widehat{BAC}=90^o\) (cmt)
=> AIOJ là hình chữ nhật (Hình bình hành có 1 góc trong bằng 90 độ là HCN)
b/
Ta có
IA=IB (Hai tiếp tuyến cùng xp từ 1 điểm thì đường thẳng nối điểm đó với tâm đường tròn vuông góc và chia đôi đường thẳng nối hai tiếp điểm)
JA=JC (Hai tiếp tuyến cùng xp từ 1 điểm thì đường thẳng nối điểm đó với tâm đường tròn vuông góc và chia đôi đường thẳng nối hai tiếp điểm)
=> IJ là đường trung bình của tg ABC => IJ//BC
c/
G là trọng tâm tg ABC \(\Rightarrow OG=\dfrac{1}{3}AO\) không đổi
=> Khi A di chuyển trên đường tròn thì G di chuyển trên đường tròn đường kính OG
\(\widehat{BAC}=90^o\)

b)
Đáp án : AIOJ là hình chữ nhật
Giải
+) ta có DA,DB là tiếp tuyến của (O)
=> D cách đều A và B ,
ta dễ dàng cm đc OA = OB => O cách đều A,B
=> OD vuông góc AB => AIO = 90o90o
chứng minh tương tự = > AJO = 90o90o
B,A,C cùng thuộc nửa mf (O) , BC là đường kính => tam giác BAC vuông tại A
=> BAC = IAJ = 90o90o
xét tam giác AIOJ có 3 góc vuông = > AIOJ là hình chữ nhật

a: Xét (O) có
DA,DB là tiếp tuyến
=>DA=DB và OD là phân giác của góc AOB(1) và DO là phân giác của góc ADB
b: OA=OB
DA=DB
=>OD là trung trực của AB
=>OD vuông góc AB tại I và I là trung điểm của AB
d: Xét (O) có
EA,EC là tiếp tuyến
=>EA=EC
mà OA=OC
nên OE là trung trực của AC và OE là phân giác của góc AOC(2)
=>OE vuông góc AC tại J và J là trung điểm của AC
Từ (1), (2) suy ra góc DOE=1/2*góc BOC=180*1/2=90 độ
Xét tứ giác AIOJ có
góc AIO=góc AJO=góc IOJ=90 độ
=>AIOJ là hình chữ nhật
e: Xét ΔABC có AI/AB=AJ/AC
nên IJ//BC

(Quá lực!!!)
E N A B C D O H L
Đầu tiên, hãy CM tam giác \(EAH\) và \(ABD\) đồng dạng.
Từ đó suy ra \(\frac{EA}{AB}=\frac{AH}{BD}\) hay \(\frac{EA}{OB}=\frac{AC}{BD}\).
Từ đây CM được tam giác \(EAC\) và \(OBD\) đồng dạng.
Suy ra \(\widehat{ECA}=\widehat{ODB}\). Do đó nếu gọi \(OD\) cắt \(EC\) tại \(L\) thì CM được \(OD⊥EC\).
-----
Đường tròn đường kính \(NC\) cắt \(EC\) tại \(F\) nghĩa là \(NF⊥EC\), hay \(NF\) song song với \(OD\).
Vậy \(NF\) chính là đường trung bình của tam giác \(AOD\), vậy \(NF\) qua trung điểm \(AO\) (là một điểm cố định) (đpcm)

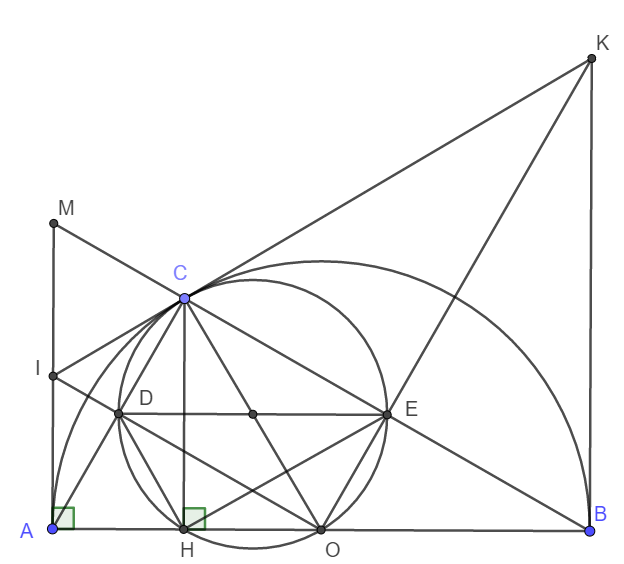
a) Do C thuộc nửa đường tròn nên \(\widehat{ACB}=90^o\) hay AC vuông góc MB.
Xét tam giác vuông AMB có đường cao AC nên áp dụng hệ thức lượng ta có:
\(BC.BM=AB^2=4R^2\)
b) Xét tam giác MAC vuông tại C có CI là trung tuyến ứng với cạnh huyền nên IM = IC = IA
Vậy thì \(\Delta ICO=\Delta IAO\left(c-c-c\right)\)
\(\Rightarrow\widehat{ICO}=\widehat{IAO}=90^o\)
Hay IC là tiếp tuyến tại C của nửa đường tròn.
c) Xét tam giác vuông AMB có đường cao AC, áp dụng hệ thức lượng ta có:
\(MB.MC=MA^2=4IC^2\Rightarrow IC^2=\frac{1}{4}MB.MC\)
Xét tam giác AMB có I là trung điểm AM, O là trung điểm AB nên IO là đường trung bình tam giác ABM.
Vậy thì \(MB=2OI\Rightarrow MB^2=4OI^2\) (1)
Xét tam giác vuông MAB, theo Pi-ta-go ta có:
\(MB^2=MA^2+AB^2=MA^2+4R^2\) (2)
Từ (1) và (2) suy ra \(4OI^2=MA^2+4R^2.\)
d) Do IA, IC là các tiếp tuyến cắt nhau nên ta có ngay \(AC\perp IO\Rightarrow\widehat{CDO}=90^o\)
Tương tự \(\widehat{CEO}=90^o\)
Xét tứ giác CDOE có \(\widehat{CEO}=\widehat{CDO}=90^o\)mà đỉnh E và D đối nhau nên tứ giác CDOE nội tiếp đường tròn đường kính CO.
Xét tứ giác CDHO có: \(\widehat{CHO}=\widehat{CDO}=90^o\) mà đỉnh H và D kề nhau nên CDHO nội tiếp đường tròn đường kính CO.
Vậy nên C, D, H , O, E cùng thuộc đường tròn đường kính CO.
Nói cách khác, O luôn thuộc đường tròn ngoại tiếp tam giác HDE.
Vậy đường tròn ngoại tiếp tam giác HDE luôn đi qua điểm O cố định.

A B O C D M E F K I N L
Gọi BE cắt đường tròn (O) tại điểm thứ hai là N. Gọi L là hình chiếu của I trên ME.
Dễ thấy ^BNA = 900. Suy ra \(\Delta\)BNA ~ \(\Delta\)BCE (g.g) => BN.BE = BC.BA
Cũng dễ có \(\Delta\)BMA ~ \(\Delta\)BCK (g.g) => BC.BA = BM.BK. Do đó BN.BE = BM.BK
Suy ra tứ giác KENM nội tiếp. Từ đây ta có biến đổi góc: ^KNA = 3600 - ^ANM - ^KNM
= (1800 - ^ANM) + (1800 - ^KNM) = ^ABM + (1800 - ^AEM) = ^EFM + ^MEF = ^KFA
=> 4 điểm A,K,N,F cùng thuộc một đường tròn. Nói cách khác, đường tròn (I) cắt (O) tại N khác A
=> OI vuông góc AN. Mà AN cũng vuông góc BE nên BE // OI (1)
Mặt khác dễ có E là trung điểm dây KF của (I) => IE vuông góc KF => IE // AB (2)
Từ (1);(2) suy ra BOIE là hình bình hành => IE = OB = const
Ta lại có EM,AB cố định => Góc hợp bởi EM và AB không đổi. Vì IE // AB nên ^IEL không đổi
=> Sin^IEL = const hay \(\frac{IL}{IE}=const\). Mà IE không đổi (cmt) nên IL cũng không đổi
Vậy I di động trên đường thẳng cố định song song với ME, cách ME một khoảng không đổi (đpcm).
ko cần vẽ hình
ok rồi thì có làm không cứ trả lời các câu hỏi như vậy