Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác MAIC có
\(\widehat{MAI}+\widehat{MCI}=90^0+90^0=180^0\)
=>MAIC là tứ giác nội tiếp
=>\(\widehat{AMC}+\widehat{AIC}=180^0\left(1\right)\)
Ta có: AM\(\perp\)AB
BN\(\perp\)AB
Do đó: AM//BN
=>\(\widehat{AMN}+\widehat{CNB}=180^0\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{CIA}=\widehat{CNB}\)
Xét (O) có
\(\widehat{CAB}\) là góc nội tiếp chắn cung CB
\(\widehat{CBN}\) là góc tạo bởi tiếp tuyến BN và dây cung BC
Do đó: \(\widehat{CAB}=\widehat{CBN}\)
Xét ΔCAI và ΔCBN có
\(\widehat{CAI}=\widehat{CBN}\)
\(\widehat{CIA}=\widehat{CNB}\)
Do đó: ΔCAI đồng dạng với ΔCBN
b: Xét tứ giác ICNB có \(\widehat{ICN}+\widehat{IBN}=90^0+90^0=180^0\)
nên ICNB là tứ giác nội tiếp
=>\(\widehat{IBC}=\widehat{INC}\)
=>\(\widehat{CBA}=\widehat{CNI}\)
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
Xét ΔCAB vuông tại C và ΔCIN vuông tại C có
\(\widehat{CBA}=\widehat{CNI}\)
Do đó: ΔCAB đồng dạng với ΔCIN
c: Ta có: MAIC là tứ giác nội tiếp
=>\(\widehat{MAC}=\widehat{MIC}\)
Ta có: NCIB là tứ gáic nội tiếp
=>\(\widehat{NIC}=\widehat{NBC}\)
Ta có: \(\widehat{MIN}=\widehat{MIC}+\widehat{NIC}\)
\(=\widehat{MAC}+\widehat{NBC}\)
\(=90^0-\widehat{CAB}+90^0-\widehat{CBA}\)
\(=180^0-90^0=90^0\)

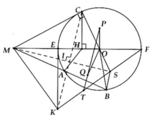
a, HS tự chứng minh
b, MH.MO = MA.MB ( = M C 2 )
=> ∆MAH:∆MOB (c.g.c)
=> M H A ^ = M B O ^
M B O ^ + A H O ^ = M H A ^ + A H O ^ = 180 0
=> AHOB nội tiếp
c, M K 2 = ME.MF = M C 2 Þ MK = MC
∆MKS = ∆MCS (ch-cgv) => SK = SC
=> MS là đường trung trực của KC
=> MS ^ KC tại trung của CK
d, Gọi MS ∩ KC = I
MI.MS = ME.MF = M C 2 => EISF nội tiếp đường tròn tâm P Þ PI = PS. (1)
MI.MS = MA.MB (= M C 2 ) => AISB nội tiếp đường tròn tâm Q Þ QI = QS. (2)
Mà IT = TS = TK (do DIKS vuông tại I). (3)
Từ (1), (2) và (3) => P, T, Q thuộc đường trung trực của IS => P, T, Q thẳng hàng
help meeeeeeeeeeeeeeeeeeeeeeee!!!