Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Chứng minh được DBOF nội tiếp đường tròn tâm I là trung điểm của DO
b, O A = O F 2 + A F 2 = 5 R 3 => cos D A B ^ = A F A O = 4 5
c, ∆AMO:∆ADB(g.g) => D M A M = O B O A
mà M O D ^ = O D B ^ = O D M ^ => DM = OM
=> D B D M = D B O M = A D A M . Xét vế trái B D D M - D M A M = A D - D M A M = 1
d, D B = A B . tan D A B ^ = 8 R 3 . 3 4 = 2 R => O M = A O . tan D A B ^ = 5 R 4
=> S O M D B = 13 R 2 8
S O M D B ngoài = S O M D B - 1 4 S O , R = R 2 8 13 - 2 π

a, Vì Mx lần lượt là tiếp tuyến (O)
=> ^PMN = 900
Ta có ^EPM = ^EMN ( cùng phụ ^PME )
Lại có cung ME = cung EN => ME = EN
=> tam giác EMN vuông cân tại E vì ^MEN = 900 ( góc nt chắn nửa đường tròn)
=> ^MPE = ^MNP mà ^PMN = 900
Vậy tam giác PMN vuông cân tại M
b, Ta có ^EFN = ^EMN ( góc nt chắn cung EN )
mà ^QPE = ^EMN (cmt)
=> ^NFE = ^QPE mà ^NFE là góc ngoài đỉnh F
Vậy tứ giác EFQP là tứ giác nt 1 đường tròn
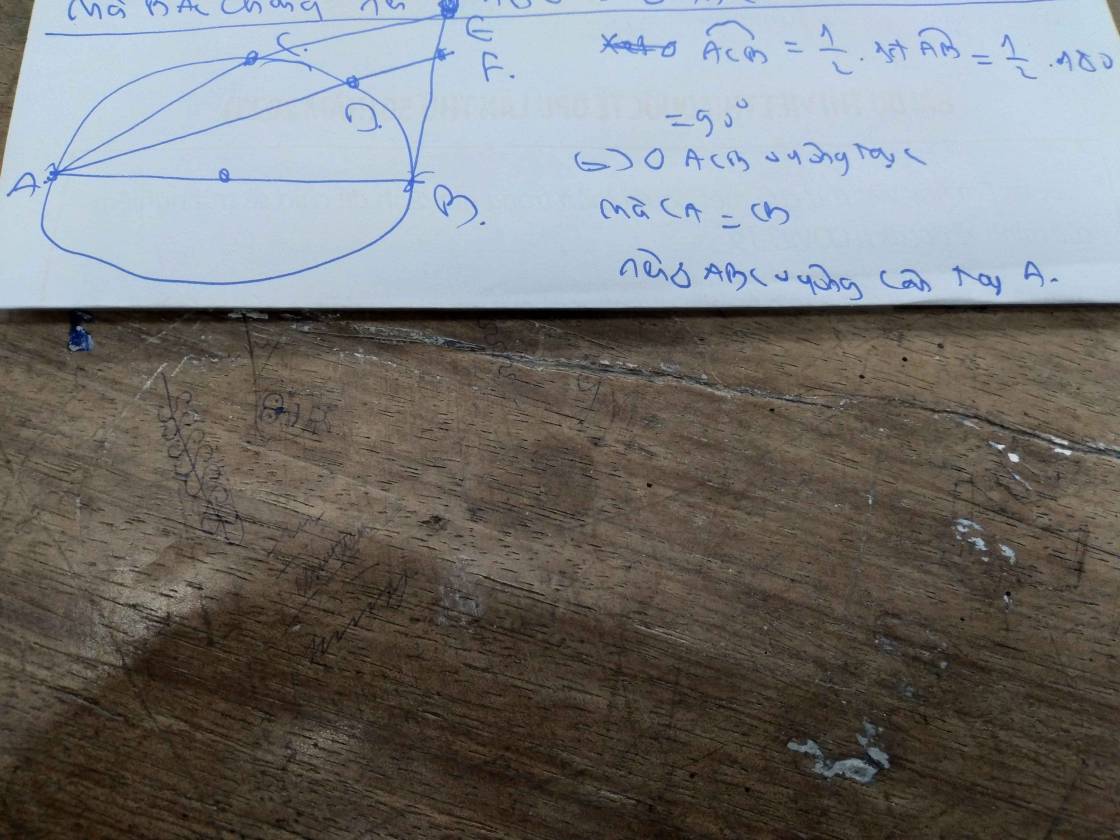


a: góc EAB=1/2*90=45 độ
=>góc AEB=45 độ
b: góc EFD=góc FAB+góc FBA=90 độ+góc DAB
góc ECD+góc ACD=180 độ
=>góc ECD=góc DBA
=>góc EFD+góc ECD=180 độ
=>CDFE nội tiếp