Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Chứng minh được ∆COD đều => A M B ^ = 60 0
b, A B C ^ = 30 0 => A O C ^ = 60 0 => l A C ⏜ = πR 3

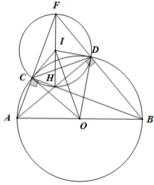
a) +)Xét đtron (O) có : CA,CM là hai tiếp tuyến cắt nhau tại C, tiếp điểm A,M
=> CA=CM ; OC là p/giác của góc AOM(T/chất hai tiếp tuyến cắt nhau)
Có: MD, BD là hai tiếp tuyến cắt nhau tại D , tiếp điểm M,B
=> MD=DB ; OD là p/giác của góc BOM
Ta có : DC= CM+MD
Mà CA=CM; MD=DB
Suy ra: CD= AC+BD
+)Vì AC là tiếp tuyến của nửa đtron (O) tại A nên CA vg góc với AB tại A
=> góc CAB= 90°
=> ∆ABC vuông tại A
b) Ta có : góc AOC= gócMOC (OC là phân giác của góc AOM
Góc MOD= BOD(OD là p/giác của BOM)
Lại có : AOC + MOC+ MOD+ BOD= 180°
SUY RA : MOC+ MOD=90°
=> COD=90°
=> ∆COD vuông tại O
Vì CD là tiếp tuyến của nửa đtron (O) tại M nên: OM vg góc với CD
Xét ∆OCD vg tại O; đường cao OM:
OM²= CM.MD (Hệ thức lượng…)
Mà OM=R (bán kính nửa đtron (O))
CA= CM; MD=MB
SUY RA : AC.BD=R²
(Vì ko tải đc ảnh nên chắc bạn phải tự vẽ hình…..câu c mình cảm tưởng đề bài ko đc đúng vì mình thấy nó khác với hình của mình(∆ABC ko đều đc)

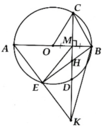
a) Vì C, D thuộc nửa đường tròn đường kính AB nên
A C B = A D B = 90 o ⇒ F C H = F D H = 90 o ⇒ F C H + F D H = 180 o
Suy ra tứ giác CHDF nội tiếp
b) Vì AH ⊥ BF, BH ⊥ AF nên H là trực tâm ∆ AFB ⇒ FH ⊥ AB
⇒ C F H = C B A ( = 90 o − C A B ) ⇒ Δ C F H ~ Δ C B A ( g . g ) ⇒ C F C B = C H C A ⇒ C F . C A = C H . C B

a) Xét ΔOCD có OC=OD(=R)
nên ΔOCD cân tại O(Định nghĩa tam giác cân)
Xét ΔOCD cân tại O có CD=OC(=R)
nên ΔOCD đều(Dấu hiệu nhận biết tam giác đều)
\(\Leftrightarrow\widehat{COD}=60^0\)
hay \(sđ\stackrel\frown{CD}=60^0\)
a, Khi M ở ngoài hay M nằm trong đường tròn thì ∆MCD và ∆MBA đều có 2 góc bằng nhau => ĐPCM
Tỷ số đồng dạng là: C D A B = 1 2
b, A B C ^ = 30 0 => A O C ^ = 60 0 => l A C ⏜ = πR 3