Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì AH, HB, AB đều là các đường kính của các nửa đường tròn (O1) , (O2) và (O) nên tứ giác MPHQ có ba góc P, Q, M vuông. Vì vậy nó là hình chữ nhật.
Từ đó, ta có HM = PQ.
b) Vì MHPQ là hình chữ nhật nên \widehat{MPQ}=\widehat{MHQ}=\widehat{MBH}\left(=\dfrac{\stackrel\frown{HQ}}{2}\right)MPQ=MHQ=MBH(=2HQ⌢), do đó APQB là tứ giác nội tiếp.
c) Ta có \widehat{O_1PA}=\widehat{PAO_1}=90^o-\widehat{HMP}=90^o-\widehat{MPQ}O1PA=PAO1=90o−HMP=90o−MPQ
\Rightarrow\widehat{O_1PA}+\widehat{MPQ}=90^o\Rightarrow\widehat{O_1PQ}=90^o⇒O1PA+MPQ=90o⇒O1PQ=90o nên PQ tiếp xúc nửa đường tròn (O1) tại P.
Tương tự , PQ tiếp xúc (O2) tại Q hay PQ là tiếp tuyến chung của hai nửa đường tròn (O1) và (O2)

a, MPHQ là hình chữ nhật => MH = PQ
b, Sử dụng hệ thức lượng trong tam giác vuông chứng minh được MP.MA = MQ.MB => ∆MPQ: ∆MBA
c, P M H ^ = M B H ^ => P Q H ^ = O 2 Q B ^ => PQ là tiếp tuyến của O 2
Tương tự PQ cũng là tiếp tuyến ( O 1 )

M A C x B D y H K O I
a) Tam giác AMC vuông tại M có MH là đường cao
\(\Rightarrow MH=\sqrt{AH.BH}\)( hệ thức lượng trong tam giác vuông )
\(\Rightarrow MH=\sqrt{15}\left(cm\right)\)
b) Vì AC song song với BD nên ta có : \(\frac{AC}{BD}=\frac{AI}{ID}=\frac{CM}{MD}\)( vì \(AC=CM;BD=MD\))
\(\Rightarrow MI//AC\)mà \(MH//AC\) ( cùng vuông góc với AB )
Suy ra \(M,I,H\)thẳng hàng
c ) Đặt \(AB=a,AM=c,BM=b\)
Ta có:
\(AK=\frac{a+c-b}{2};BK=\frac{a+b-c}{2}\)
\(\Rightarrow AK.BK=\frac{a+c-b}{2}.\frac{a+b-c}{2}=\frac{1}{2}.\left[\frac{\left(a+c-b\right)\left(a+b-c\right)}{2}\right]\)
\(=\frac{1}{2}\left[\frac{a^2-\left(b-c\right)^2}{2}\right]=\frac{1}{2}\left[\frac{a^2-\left(b^2+c^2\right)+2bc}{2}\right]\)
\(=\frac{1}{2}.\frac{2bc}{2}=\frac{1}{2}.bc=\frac{1}{2}AM.MB=S_{AMB}\)
Vậy \(S_{AMB}=AK.KB\)
Chúc bạn học tốt !!!

Giải:
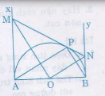
a) Ta có OM, ON lần lượt là tia phân giác cả AOP và BOP
Mà AOP kể bù BOP nên suy ra OM vuông góc với ON.
Vậy ∆MON vuông tại O.
Lại có ∆APB vuông vì có góc vuông (góc nội tiếp chắn nửa cung tròn)
Tứ giác AOPM nội tiếp đường tròn vì có +
= 2v. Nên
=
(cùng chắn cung OP).
Vậy hai tam giác vuông MON à APB đồng dạng vị có cắp góc nhọn bằng nhau.
b)
Tam giác AM = MP, BN = NP (1) (tính chất hai tiếp tuyến cắt nhau)
Tam giác vuông MON có OP là đường cao nên:
MN.PN = OP2 (2)
Từ 1 và 2 suy ra AM.BN = OP2 = R2
c) Từ tam giác MON đồng dạng với tam giác APB ta có :
Khi AM = thi do AM.BN = R2 suy ra BN = 2R
Do đó MN = MP + PN = AM + BN = + 2R =
Suy ra MN2 =
Vậy =
d) Nửa hình tròn APB quay quanh bán kính AB = 2R sinh ra một hình cầu có bán kính R.
Vậy V = πR3

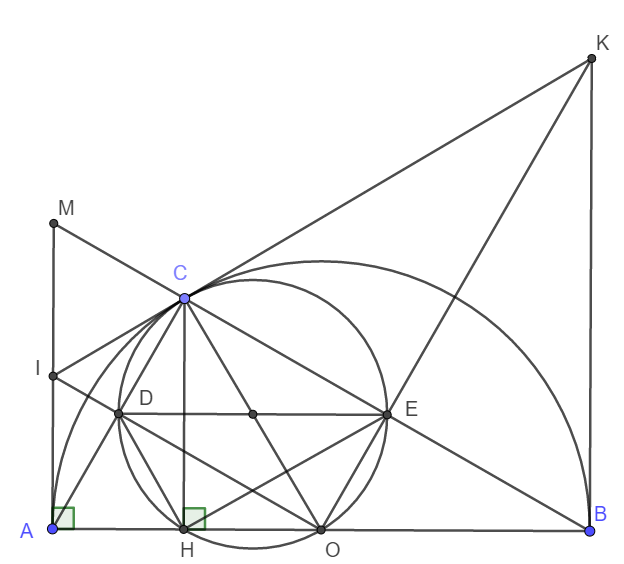
a) Do C thuộc nửa đường tròn nên \(\widehat{ACB}=90^o\) hay AC vuông góc MB.
Xét tam giác vuông AMB có đường cao AC nên áp dụng hệ thức lượng ta có:
\(BC.BM=AB^2=4R^2\)
b) Xét tam giác MAC vuông tại C có CI là trung tuyến ứng với cạnh huyền nên IM = IC = IA
Vậy thì \(\Delta ICO=\Delta IAO\left(c-c-c\right)\)
\(\Rightarrow\widehat{ICO}=\widehat{IAO}=90^o\)
Hay IC là tiếp tuyến tại C của nửa đường tròn.
c) Xét tam giác vuông AMB có đường cao AC, áp dụng hệ thức lượng ta có:
\(MB.MC=MA^2=4IC^2\Rightarrow IC^2=\frac{1}{4}MB.MC\)
Xét tam giác AMB có I là trung điểm AM, O là trung điểm AB nên IO là đường trung bình tam giác ABM.
Vậy thì \(MB=2OI\Rightarrow MB^2=4OI^2\) (1)
Xét tam giác vuông MAB, theo Pi-ta-go ta có:
\(MB^2=MA^2+AB^2=MA^2+4R^2\) (2)
Từ (1) và (2) suy ra \(4OI^2=MA^2+4R^2.\)
d) Do IA, IC là các tiếp tuyến cắt nhau nên ta có ngay \(AC\perp IO\Rightarrow\widehat{CDO}=90^o\)
Tương tự \(\widehat{CEO}=90^o\)
Xét tứ giác CDOE có \(\widehat{CEO}=\widehat{CDO}=90^o\)mà đỉnh E và D đối nhau nên tứ giác CDOE nội tiếp đường tròn đường kính CO.
Xét tứ giác CDHO có: \(\widehat{CHO}=\widehat{CDO}=90^o\) mà đỉnh H và D kề nhau nên CDHO nội tiếp đường tròn đường kính CO.
Vậy nên C, D, H , O, E cùng thuộc đường tròn đường kính CO.
Nói cách khác, O luôn thuộc đường tròn ngoại tiếp tam giác HDE.
Vậy đường tròn ngoại tiếp tam giác HDE luôn đi qua điểm O cố định.