Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, xét tứ giác ACMD có:
góc DAC + góc DMC=180 độ( do DAC=90 độ, CMD =90 độ)
vậy ACMD là tứ giác nt
xét tứ giác BCME có:
góc CBE+ góc CME= 180 độ( vì góc CBE= 90 độ, góc CME =90 độ)
vậy tứ giác BCME là tg nt

a: góc DAC+góc DMC=180 độ
=>DACM nội tiếp
góc EMC+góc EBC=180 độ
=>EMCB nội tiếp
b: DACM nội tiếp
=>góc MDC=góc MAC
=>góc MDC=góc MAB
EMCB nội tiếp
=>góc MEC=góc MBC=góc MBA
c: góc DCM+góc ECM
=góc DAM+góc EBM
=90 độ-góc MAB+90 độ-góc MBA
=góc AMB=90 độ
=>góc DCE=90 độ
=>ΔCDE vuông tại C

Bạn tự vẽ hình nha
a)
Xét tứ giác ACMD có :DAC=90 , DMC=90
DAC +DMC =180
nên ACMD là tứ giác nội tiếp
Xét tứ giác BCME có: CME=90 ,CBE=90
CME + CBE = 180
nên BCME là tứ giác nội tiếp
b)
Theo a ta có :BCME là tứ giác nội tiếp nên MEC=MBC (cùng chắn cung MC)
ACMD là tứ giác nội tiếp nên MDC=MAC (cùng chắn cung MC )

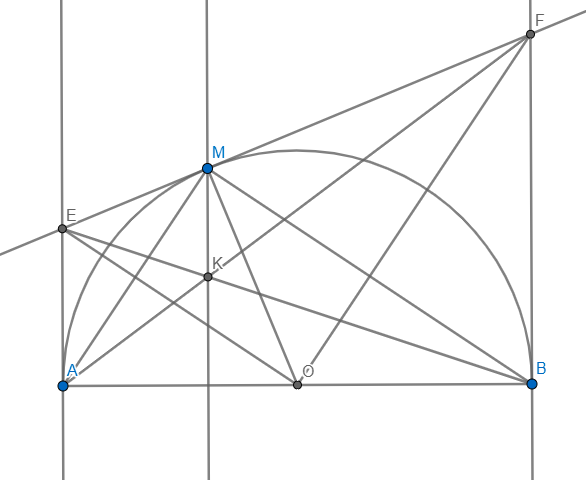
1) Vì EM,EA là tiếp tuyến \(\Rightarrow OE\) là phân giác \(\angle MOA\)
\(\Rightarrow\angle MOE=\dfrac{1}{2}\angle MOA\)
Vì FM,FB là tiếp tuyến \(\Rightarrow OF\) là phân giác \(\angle MOB\)
\(\Rightarrow\angle MOF=\dfrac{1}{2}\angle MOB\)
\(\Rightarrow\angle MOE+\angle MOF=\dfrac{1}{2}\left(\angle MOA+\angle MOB\right)=\dfrac{1}{2}.180=90\)
\(\Rightarrow\angle EOF=90\)
2) Ta có: \(\angle EAO+\angle EMO=90+90=180\Rightarrow AEMO\) nội tiếp
\(\Rightarrow\angle MEO=\angle MAO\)
Vì AB là đường kính \(\Rightarrow\angle AMB=90\)
Xét \(\Delta MAB\) và \(\Delta OEF:\) Ta có: \(\left\{{}\begin{matrix}\angle AMB=\angle EOF\\\angle FEO=\angle MAB\end{matrix}\right.\)
\(\Rightarrow\Delta MAB\sim\Delta OEF\left(g-g\right)\)
Vì \(AE\parallel BF(\bot AB)\) \(\Rightarrow\dfrac{BF}{AE}=\dfrac{FK}{AK}\left(1\right)\)
Vì EM,EA là tiếp tuyến \(\Rightarrow EA=EM\left(2\right)\)
Vì FM,FB là tiếp tuyến \(\Rightarrow FB=FM\left(3\right)\)
Thế (2),(3) vào (1) \(\Rightarrow\dfrac{FM}{EM}=\dfrac{FK}{AK}\Rightarrow\) \(MK\parallel AE\) \(\Rightarrow MK\bot AB\)

a: Xét (O) có
CM là tiếp tuyến có M là tiếp điểm
CA là tiếp tuyến có A là tiếp điểm
Do đó: CM=CA
Xét (O) có
DM là tiếp tuyến có M là tiếp điểm
DB là tiếp tuyến có B là tiếp điểm
Do đó: DM=DB
Ta có: CM+MD=CD
nên CD=CA+DB

a: Xét (O) có
CM là tiếp tuyến
CA là tiếp tuyến
Do đó: CM=CA
Xét (O) cso
DM là tiếp tuyến
DB là tiếp tuyến
DO đó: DM=DB
Ta có: CM+MD=CD
mà CM=CA
và MD=DB
nên CD=CA+DB
b: Xét tứ giác DMOB có
\(\widehat{DMO}+\widehat{DBO}=180^0\)
Do đó: DMOB là tứ giác nội tiếp