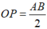Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


* Kết luận :
Quỹ tích các điểm D khi C chạy trên nửa đường tròn đường kính AB là đường tròn đường kính OP, với \(OP=\dfrac{AB}{2}\)

Bạn tự vẽ hình
1. Gọi \(K\) là điểm chính giữa của nửa đường tròn. Xét hai tam giác \(\Delta KOD\) và \(\Delta OCH\) có \(OK=CO=R\), \(\angle KOD=\angle OCH\) (so le trong) và \(OD=CH\) (giả thiết). Suy ra hai tam giác \(\Delta KOD\) và \(\Delta OCH\)
bằng nhau (c.g.c). Do đó \(\angle KDO=90^{\circ}\to D\) nằm trên đường tròn đường kính OK.
Khi C trùng A thì D trùng với O và khi C trùng với B thì D trùng với O. Do đó tập hợp D sẽ là toàn bộ đường tròn đường kính OK.
2. Kéo dài tia DC cắt (O) ở điểm thứ hai T. Do tứ giác ACTB nội tiếp nên góc TBA = góc DCA = 60 độ. Vậy T là điểm cố định. Do tam giác ACD đều và M là trung điểm CD nên AM vuông góc với CD. Suy ra M nhìn đoạn AT dưới 1 góc vuông. Vậy M nằm trên đường tròn đường kính AT.
Vì C chỉ chạy trên nửa đường tròn, khi C trùng A thì M trùng A và khi C trùng với B thì M trùng với T. Vậy M chạy trên nửa đường tròn đường kính AT, trong nửa mặt phẳng không chứa điểm B.
Chỉ vậy thôi.


Khi C chuyển động trên nửa đường tròn đường kính AB cố định thì C chuyển động trên cung chứa góc 45 ° dựng trên đoạn thẳng AB.Khi đó dây AC thay đổi phụ thuộc vào vị trí điểm C trên nửa đường tròn đường kính AB
- dây AC lớn nhất bằng đường kính của đường tròn .Khi C trùng với B thì D cũng trùng với B.vậy B là điểm của quỹ tích
- Dây AC nhỏ nhất có độ dài bằng 0 khi C trùng với A.Khi đó D trùng với B’ là giao điểm của tiếp tuyến đường tròn đường kính AB tại A với cung chứa góc 45 ° vẽ trên AB
*Chứng minh đảo:
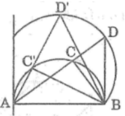
Lấy điểm D’ bất kì trên cung BB' ,nối AD’ cắt đường tròn đường kính AB tại C’.Nối BC’ ,B’D’

Quỹ tích điểm các điểm D khi C chuyển động trên nửa đường tròn đường kính AB là cung BB’ nằm trên cung chứa góc 45 ° vẽ trên đoạn AB, trong nửa mặt phẳng bờ AB có chứa điểm C (bị giới hạn bởi tiếp tuyến Ax).

*chứng minh thuận
Trong đường tròn đường kính AB ta có:

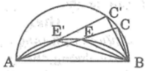
Khi C chuyển động trên đường tròn đường kính AB cố định thì D chuyển động trên cung chứa góc 135 ° dựng trên đoạn thẳng AB cố định
-Khi dây AC có độ dài lớn nhất bằng đường kính đường tròn thì C trùng với B nên E cũng trùng với B.Vậy B là điểm thuộc quỹ tích
- Khi dây AC có độ dài nhỏ nhất bằng 0 thì C trùng với A.khi đó E trùng với A nên A là một điểm của quỹ tích
Vậy E chuyển động trên cung chứa góc 135 ° vẽ trên đoạn AB nằm trên nửa mặt phẳng bờ AB chứa điểm C
*chứng minh đảo:
Lấy điểm E’ bất kì trên cung chứa góc 135 ° , nối AE’ cắt đường tròn đường kính AB tại C’.Nối BE’, BC’

Quỹ tích điểm các điểm E khi C chuyển động trên nửa đường tròn đường kính AB là cung chứa góc 135 ° vẽ trên đoạn AB, trong nửa mặt phẳng bờ AB có chứa điểm C




*Chứng minh thuận:
Từ O kẻ đường thẳng vuông góc với AB cắt nửa đường tròn đường kính AB tại P.
Vì O cố dịnh, đường tròn đường kính AB cố định nên P cố định.Nối PD
Ta có: OP // CH (cùng ⊥ AB)
Xét hai tam giác HCO và DOP ta có:
OD = CH (gt)
Khi C chuyển động trên nửa đường tròn đường kính AB thì D thay đổi tạo với hai đầu đọan thẳng OP cố định một góc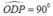
Vậy D chuyển động trên đường tròn đường kính OP
*Chứng minh đảo
Lấy điểm D’ bất kì trên đường tròn đường kính OP ,nối OD’ cắt nửa đường tròn đường kính AB tại C’.Nối PD’ và C’H’ ⊥ AB
Xét hai tam giác C’H’O và PD’O ta có:
Vậy △ C’H’O = △ PD’O (c.g.c) ⇒ C’H’ = OD’
Quỹ tích điểm các điểm D khi C chuyển động trên nửa đường tròn đường kính AB là đường tròn đường kính OP, với