Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: ΔOAM cân tại O
mà OC là trung tuyến
nên OC vuông góc AM
góc OBN+góc OCN=180 độ
=>OCNB nội tiếp
2: Xét ΔACO vuông tại C và ΔABN vuông tại B có
góc CAO chung
=>ΔACO đồng dạng với ΔABN
=>AC/AB=AO/AN
=>AC*AN=AO*AB

a) Xét (O) có
ΔBMA nội tiếp đường tròn(B,M,A∈(O))
BA là đường kính(gt)
Do đó: ΔBMA vuông tại M(Định lí)
Xét (O) có
AB là đường kính của (O)(gt)
nên O là trung điểm của AB
Xét ΔBMA có
O là trung điểm của AB(gt)
C là trung điểm của AM(gt)
Do đó: OC là đường trung bình của ΔBMA(Định nghĩa đường trung bình của tam giác)
⇒OC//BM và \(OC=\dfrac{BM}{2}\)(Định lí 2 về đường trung bình của tam giác)
Ta có: OC//BM(cmt)
BM⊥BA(ΔBMA vuông tại M)
Do đó: OC⊥AM(Định lí 2 từ vuông góc tới song song)
Xét tứ giác OCNB có
\(\widehat{OCN}\) và \(\widehat{OBN}\) là hai góc đối
\(\widehat{OCN}+\widehat{OBN}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: OCNB là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
b) Xét ΔNBA vuông tại B và ΔOCA vuông tại C có
\(\widehat{OAC}\) chung
Do đó: ΔNBA∼ΔOCA(g-g)
⇒\(\dfrac{AB}{AC}=\dfrac{AN}{AO}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AC\cdot AN=AO\cdot AB\)(đpcm)
c) Ta có: OC⊥AN(cmt)
mà E∈OC(gt)
nên EC⊥NA
Xét ΔNEA có
EC là đường cao ứng với cạnh NA(cmt)
AB là đường cao ứng với cạnh NE(gt)
EC cắt AB tại O(gt)
Do đó: O là trực tâm của ΔNEA(Định lí ba đường cao của tam giác)
⇒NO⊥AE(đpcm)

a) OBNC có NCO=OBN=90 nên OBNC là tứ giác nội tiếp
b) Xét tam giác ADC có AB,DC là các đường cao
mà AB cắt DC tại O
suy ra O là trực tâm của tam giác ADC
nên NO vuông góc với AD
c)
CONB là tứ giác nôi tiếp nên COA=CNB
Xét tam giác ACO và tam giác DCN
COA=CNB(cmt)
ACO=NCD=90
nên tam giác ACO đồng dạng với tam giác DNC
nên CA.CN=CO.CD
Còn câu d mk chịu

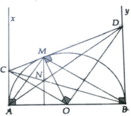
a, Từ CA, CM là tiếp tuyến của (O) chứng minh được A,C,M,O ∈ đường tròn bán kính O C 2
b, Chứng minh OC,BM cùng vuông góc với AM . từ đó suy ra OC//BM
c, S A C D B = A C + B D A B 2 = A D . A B 2
=> S A C D B nhỏ nhất khi CD có độ dài nhỏ nhất
Hay M nằm chính giữa cung AB
d, Từ tính chất hai giao tuyến => AC = CM và BM=MD, kết hợp với AC//BD
ta chứng minh được C N N B = C M M D => MN//BD => MN ⊥ AB

Câu a dễ nha: tứ giác BCDO có DOB+DCB=90+90=180(mà 2 góc ở vị trí đối nhau )
nên BCDO nội tiếp
câu b) tam giác ADO và tam giác ABC có:
góc BAC chung
AOD=ACB=90
câu c: CB là dây cung mà OE là đường thẳng đi qua bán kính nên OE vuông góc với BC
nên OE// DC hay AD//OE mà DE//AO nên OEDA là hình bình hành
câu d thì mk chưa nghĩ ra hihi thông cảm nha
ở câu c nếu chỉ có BC là dây và OE là đường thẳng đi qua bán kính thì BC chưa thể vuông góc với OE được bạn nhé mà cần phải OE đi qua trung điểm của BC nữa

(Quá lực!!!)
Đầu tiên, hãy CM tam giác \(EAH\) và \(ABD\) đồng dạng.
Từ đó suy ra \(\frac{EA}{AB}=\frac{AH}{BD}\) hay \(\frac{EA}{OB}=\frac{AC}{BD}\).
Từ đây CM được tam giác \(EAC\) và \(OBD\) đồng dạng.
Suy ra \(\widehat{ECA}=\widehat{ODB}\). Do đó nếu gọi \(OD\) cắt \(EC\) tại \(L\) thì CM được \(OD⊥EC\).
-----
Đường tròn đường kính \(NC\) cắt \(EC\) tại \(F\) nghĩa là \(NF⊥EC\), hay \(NF\) song song với \(OD\).
Vậy \(NF\) chính là đường trung bình của tam giác \(AOD\), vậy \(NF\) qua trung điểm \(AO\) (là một điểm cố định) (đpcm)
tk mk nha mọi người
Chj ơi chj giải ra bài này chưa ak
Nếu ra rồi chj có thể giải giúp e câu c k ạ