OS
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
0
HT
2
AT
28 tháng 12 2018
Theo bđt Δ có: m < n + p; n < m + p; p < m + n
=> m2 < m(n+p) = mn + pm (1)
n2 < n(m+p) = mn + np (2)
p2 < p(m+n) = pm + np (3)
Cộng theo vế 3 bđt trên
=> m2 + n2 + p2 < mn + pm + mn + np + pm + np = 2(mn + np + pm)
=> đpcm
NT
3
HP
26 tháng 4 2017
m<n+p(bđt \(\Delta\) )=> m2<m(n+p),chứng minh tương tự rồi cộng lại
26 tháng 4 2017
Vì m;n;p là 3 cạnh của 1 tam giác nên ta có : \(\hept{\begin{cases}m+n>p\\m+p>n\\n+p>m\end{cases}}\) (bđt Tam Giác)
\(\Rightarrow\hept{\begin{cases}p\left(m+n\right)>p^2\\n\left(m+p\right)>n^2\\m\left(n+p\right)>m^2\end{cases}\Rightarrow\hept{\begin{cases}mp+np>p^2\\mn+np>n^2\\mn+mp>m^2\end{cases}}}\)
\(\Rightarrow2\left(mn+np+mp\right)>m^2+n^2+p^2\)
Hay \(m^2+n^2+p^2< 2\left(mn+np+mp\right)\) (ĐFCM)
NL
1
NK
9 tháng 4 2016
Xét hiệu: 2.(mn+np+pm)- (m^2+n^2+p^2)
= m.(m+p-n) +n.(m+p-n) + p.(m+n-p)
m,n,p là độ dài 3 cạnh của 1 tam giác
=> m,n,p >0 ; m+n-p>0 ; m+p-n>0 ; n+p-m >0
=> m.(m+p-n) +n.(m+p-n) + p.(m+n-p) >0
=>2.(mn+np+pm)- (m^2+n^2+p^2) >0
=> m2 + n2 + p2 < 2.(mn+np+pm)
D
21 tháng 2 2016
\(A=\frac{\sqrt{x}+1}{\sqrt{x}-2}=\frac{\sqrt{x}-2+3}{\sqrt{x}-2}=1+\frac{3}{\sqrt{x}-2}\Rightarrow\)3 p chia hết cho \(\sqrt{x}-2\)để A là số nguyên dương
\(Ư_{\left(3\right)}\in\left\{1;-1;3;-3\right\}\Rightarrow\sqrt{x}-2\in\left\{1;3\right\}vìaplàsốnguyêndương\)
ta có : \(\sqrt{x}-2=1\Rightarrow\sqrt{x}=3\Rightarrow x=9\)
\(\sqrt{x}-2=3\Rightarrow\sqrt{x}=5\Rightarrow x=25\)
vậy để A là số nguyên dương thì x=9, x=25
TT
1
17 tháng 9 2023
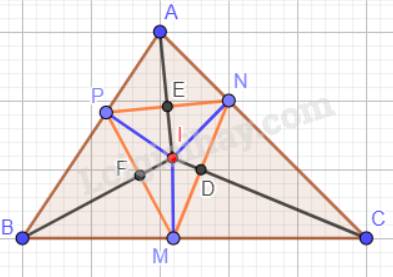
Gọi D là giao điểm của IC và MN; E là giao điểm của IA và PN; F là giao điểm của IB và PM.
Ta có: Trong tam giác ABC, ba đường phân giác cùng đi qua một điểm và điểm đó cách đều ba cạnh của tam giác hay IM = IN = IP.
Xét tam giác vuông INC và tam giác vuông IMC:
IC chung;
IN = IM.
Vậy \(\Delta INC = \Delta IMC\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {MIC} = \widehat {NIC}\)( 2 góc tương ứng).
Tương tự: \(\Delta IPA = \Delta INA\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {PIA} = \widehat {NIA}\)( 2 góc tương ứng).
\(\Delta IPB = \Delta IMB\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {PIB} = \widehat {MIB}\)( 2 góc tương ứng).
Xét hai tam giác IDN và IDM có:
ID chung;
\(\widehat {NID} = \widehat {MID}\);
IN = IM.
Vậy \(\Delta IDN = \Delta IDM\)(c.g.c)
\(\Rightarrow DN = DM\) ( 2 cạnh tương ứng);
\(\widehat {IDN} = \widehat {IDM}\) ( 2 góc tương ứng)
Mà \(\widehat {IDN} + \widehat {IDM}=180^0\) ( 2 góc kề bù)
\(\Rightarrow \widehat {IDN} = \widehat {IDM}= 180^0:2=90^0\).
Suy ra: IC là đường trung trực của cạnh MN.
Tương tự ta có:
IA là đường trung trực của cạnh PN; IB là đường trung trực của cạnh PM.
Theo BĐT tam giác:
(*)m+n>p
<=>(m+n).p>p2
<=>mp+np>p2 (p>0) (1)
(*)m+p>n
<=>(m+p).n>n2
<=>mn+pn>n2 (n>0) (2)
(*)n+p>m
<=>(n+p).m>m2
<=>mn+pm>m2 (m>0) (3)
Cộng từng vế các BĐT (1);(2);(3)
=>mp+np+mn+pn+mn+pm>m2+n2+p2
=>(mp+mp)+(pn+pn)+(mn+mn)>m2+n2+p2
=>2mp+2pn+2mn>m2+n2+p2
=>2(mn+np+pm)>m2+n2+p2
=>2(m2+n2+p2)-2(mn+np+pm)<m2+n2+p2
=>m2+n2+p2<2(mn+np+pm) (đpcm)
bn bỏ cái dòng thứ 2 từ dưới lên giúp mk nhé