Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo định lý py ta go ta có :
\(NI^2=MN^2+MI^2\)
\(NI^2=6^2+8^2\)
\(NI^2=100\)
\(\Rightarrow NI=10cm\)
b )
Xét \(\Delta DMI\) và \(DEI\) có :
\(DMI=DEI\left(90\right)\)
\(DI\) cạnh chung
\(I_1=I_2\left(gt\right)\)
\(\Rightarrow\Delta DMI=\Delta DEI\left(ch-gn\right)\)
\(\Rightarrow DM=DE\) ( 2 cạnh t ứng )
a) \(\Delta MNI\) vuông tại M, theo định lí Py-ta-go
Ta có: NI2 = MN2 + MI2
NI2 = 62 + 82
NI2 = 100
\(\Rightarrow NI=\sqrt{100}=10\left(cm\right)\).
b) Xét hai tam giác vuông MID và EID có:
ID: cạnh huyền chung
\(\widehat{I_1}=\widehat{I_2}\left(gt\right)\)
Vậy: \(\Delta MID=\Delta EID\left(ch-gn\right)\)
Suy ra: DM = DE (hai cạnh tương ứng).
c) Ta có: MI = EI (\(\Delta MID=\Delta EID\))
\(\Rightarrow\) \(\Delta MIE\) cân tại I
\(\Rightarrow\) ID là đường phân giác đồng thời là đường trung trực của ME (1)
Ta lại có: hai đường cao MN và AE cắt nhau tại D
\(\Rightarrow\) D là trực tâm của \(\Delta ANI\)
\(\Rightarrow\) ID là đường cao còn lại của \(\Delta ANI\) hay ID \(\perp\) AN (2)
Từ (1) và (2) suy ra: AN // EM (đpcm).

Xét tam giác AMN có góc MAN = 1200 suy ra tam giác AMN cân tại A
suy ra góc AMN=góc ANM = 300
Xét tam giác AHM và tam giác AHN
có AH chung
góc AHM = góc AHN = 900
AM=AN (vì tam giác AMN cân tại A)
suy ra tam giác AHM = tam giác AHN ( cạnh huyền-cạnh góc vuông)
suy ra góc MAH=góc HAN (hai góc tương ứng)
suy ra AH là tia phân giác của góc MAN
b) Xét tam giác vuong AHD và tam giác vuông AhE
có AH chung
góc hAD=góc HAE (CMT)
suy ra tam giác AHD = tam giác AHE ( cạnh huyền-góc nhọn) (1)
suy ra AD=AE suy ra tam giác ADE cân tại A
suy ra góc ADE=góc AED=300
suy ra góc ADE = góc AMN = 300
mà góc ADE đồng vị với góc AMN
suy ra DE//MN
c) tam giác HEN vuông tại E suy ra góc EHN = 600
tam giác HDM vuông tại D suy ra góc DHM = 600
mà góc DHM + góc DHE + góc EHN = 1800
suy ra góc DHE = 600 (2)
Từ (1) suy ra DH = HE suy ra tam giác DHE cân tại H (3)
Từ (2) và (3) suy ra tam giác DHE đều
d) Xét tam giác MIN vuoog tại N suy ra góc NIM = 600
góc IAN kề bù với góc NAM
suy ra góc NAI = 600
tam giác ANI có góc AIN=góc ANI=góc IAN = 600
suy ra tam giác ANI đều
suy ra AI = NI = 10cm

tu ve hinh :
xet tamgiac AMN can tai A (gt) => goc AMN = goc ANM va AM = AN (dn)
AH vuong goc voi MN => goc AHN = goc AHM = 90o (dn)
=> tamgiac AMH = tamgiac ANH (ch - gn)
=> goc NAH = goc MAH (dn) ma AH nam giua AN va AM
=> AH la phan giac cua goc MAN

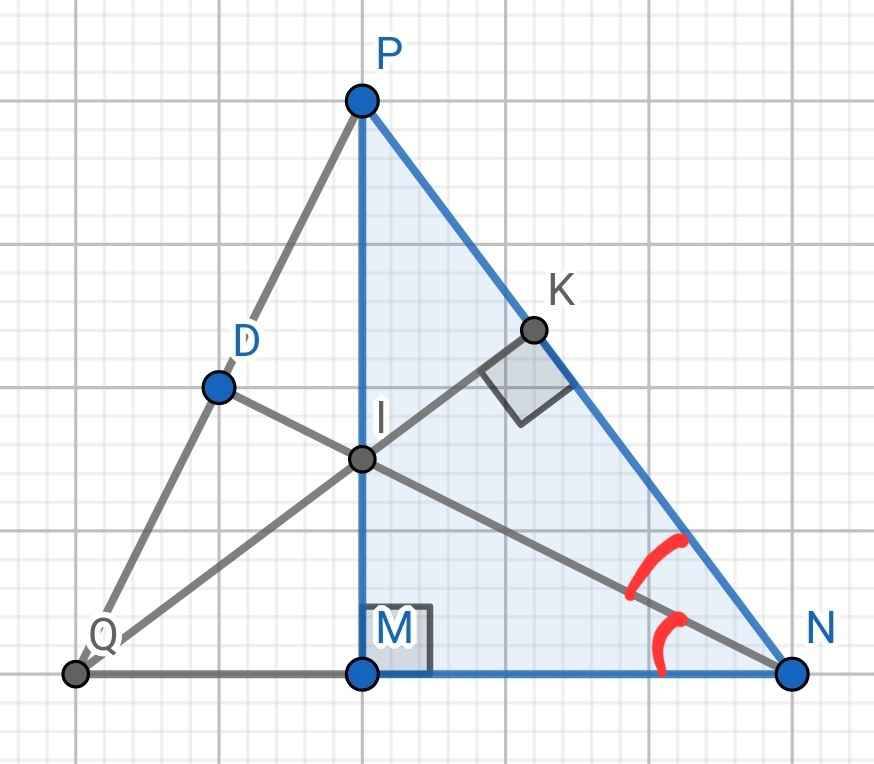
a) Xét hai tam giác vuông: ∆IMN và ∆IKN có:
IN chung
MNI = KNI (do NI là phân giác của ∠MNP)
⇒ ∆IMN = ∆IKN (cạnh huyền - góc nhọn)
b) ∆IKP vuông tại K
IP là cạnh huyền nên IP lớn nhất
IK < IP (1)
Do ∆IMN = ∆IKN (cmt)
⇒ MI = IK (2)
Từ (1) và (2)⇒ MI < IP
c) Xét hai tam giác vuông: ∆IKP và ∆IMQ có:
IM = IK (cmt)
∠PIK = ∠MIQ (đối đỉnh)
∆IKP = ∆IMQ (cạnh góc vuông - góc nhọn kề)
⇒ KP = MQ (hai cạnh tương ứng) (3)
Do ∆IMN = ∆IKN (cmt)
⇒ MN = KN (hai cạnh tương ứng) (4)
Từ (3) và (4) ⇒ KN + KP = MN + MQ
NP = NQ
⇒ ∆NPQ cân tại N
Lại có NI là phân giác của ∠MNP
⇒ NI là phân giác của ∠QNP
⇒ NI cũng là đường cao của ∆NPQ (tính chất tam giác cân)
⇒ ND ⊥ QP
Bạn tự vẽ hình nha!!!
a.
Tam giác MNI vuông tại M có:
\(NI^2=MI^2+MN^2\)
\(NI^2=8^2+6^2\)
\(NI^2=64+36\)
\(NI^2=100\)
\(NI=\sqrt{100}\)
\(NI=10\)
b.
Xét tam giác MDI vuông tại M và tam giác EDI vuông tại E có:
ID là cạnh chung
MID = EID (ID lad tia phân giác của MIE)
=> Tam giác MDI = Tam giác EDI (cạnh huyền - góc nhọn)
=> DM = DE (2 cạnh tương ứng)
c.
IM = IE (Tam giác MDI = Tam giác EDI)
=> Tam giác IME cân tại A
Xét tam giác DAM và tam giác DNE có:
DEN = DMA ( = 90 )
DE = DM (theo câu b)
NDE = ADM (2 góc đối đỉnh)
=> Tam giác DAM = Tam giác DNE (g.c.g)
Ta có:
IA = IM + MA
IN = IE + EN
mà IM = IE (Tam giác IME cân tại I)
MA = NE (Tam giác DAM = Tam giác DNE)
=> IA = IN
=> Tam giác IAN cân tại I
=> \(IAN=\frac{180-AIN}{2}\) (1)
Tam giác IME cân tại I
=> \(IME=\frac{180-MIE}{2}\) (2)
Từ (1) và (2)
=> IAN = IME
mà 2 góc này ở vị trí đồng vị
=> ME // AN