Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Gọi \(M\left( {a;b} \right) \Rightarrow \overrightarrow {AM} = \left( {a - 2;b - 3} \right)\)
Tọa độ vecto \(\overrightarrow {BC} = \left( {4; - 2} \right)\)
Để \(\overrightarrow {AM{\rm{ }}} = {\rm{ }}\overrightarrow {BC} \Leftrightarrow \left\{ \begin{array}{l}a - 2 = 4\\b - 3 = - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 6\\b = 1\end{array} \right.\)
Vậy để \(\overrightarrow {AM{\rm{ }}} = {\rm{ }}\overrightarrow {BC} \) thì tọa độ điểm M là:\(M\left( {6;1} \right)\)
b) Gọi \(N\left( {x,y} \right) \Rightarrow \overrightarrow {NC} = \left( {3 - x, - 1 - y} \right)\)và \(\overrightarrow {AN} = \left( {x - 2,y - 3} \right)\)
Do N là trung điểm AC nên \(\overrightarrow {AN} = \overrightarrow {NC} \Leftrightarrow \left\{ \begin{array}{l}x - 2 = 3 - x\\y - 3 = - 1 - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{5}{2}\\y = 1\end{array} \right.\) . Vậy \(N\left( {\frac{5}{2},1} \right)\)
Ta có: \(\overrightarrow {BN} {\rm{ }} = \left( { \frac{7}{2};0} \right)\) và \(\overrightarrow {NM} = \left( {\frac{{ 7}}{2};0} \right)\). Vậy \(\overrightarrow {BN} {\rm{ }} = {\rm{ }}\overrightarrow {NM} \)

a) Dựa vào hình vẽ, ta có: \({x_A} = 2,{y_A} = 2\) và \({x_B} = 4,{y_B} = 3\)
b) Để \(\overrightarrow {OM} {\rm{ }} = {\rm{ }}\overrightarrow {AB} \) thì điểm M phải có tọa độ: \(M\left( {1;2} \right)\). Do đó, toạn độ của vectơ\(\overrightarrow {AB} \)là \(\overrightarrow {AB} = \left( {2;1} \right)\)
c) Do \(\overrightarrow {AB} = \left( {2;1} \right)\) nên \(a = 2,b = 1\)
Ta có: \({x_B} - {x_A} = 4 - 2 = 2\), \({y_B} - {y_A} = 3 - 2 = 1\)
Vậy \({x_B} - {x_A} = a\) và \({y_B} - {y_A} = b\)

Để xác định điểm A, ta làm như sau (Hình 8):
• Qua O kẻ đường thẳng d song song với giá của vectơ \(\overrightarrow u \).
• Lấy điểm A trên đường thẳng d sao cho hai vectơ \(\overrightarrow {OA} \), \(\overrightarrow u \) cùng hướng và độ dài đoạn thẳng OA bằng độ dài vectơ \(\overrightarrow u \).

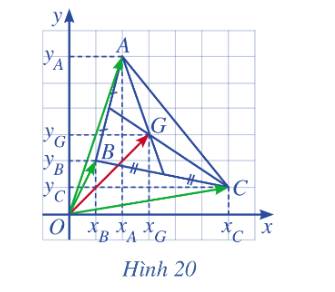
a) Ta có vectơ \(\overrightarrow {OG} \) theo ba vectơ \(\overrightarrow {OA} \) , \(\overrightarrow {OB} \)và \(\overrightarrow {OC} \) là: \(\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right)\)
b) Do tọa độ ba điểm A , B và C là: \(A\left( {{x_A},{y_A}} \right),B\left( {{x_B},{y_B}} \right),C\left( {{x_C},{y_C}} \right)\) nên ta có:\(\overrightarrow {OA} = \left( {{x_A},{y_A}} \right),\overrightarrow {OB} = \left( {{x_B},{y_B}} \right),\overrightarrow {OC} = \left( {{x_C},{y_C}} \right)\)
Vậy\(\overrightarrow {OG} = \frac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right) = \frac{1}{3}\left( {{x_A} + {x_B} + {x_C};{y_A} + {y_B} + {y_C}} \right) = \left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)\)
Tọa độ điểm G chính là tọa độ của vectơ \(\overrightarrow {OG} \) nên tọa độ G là \(G\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)\)

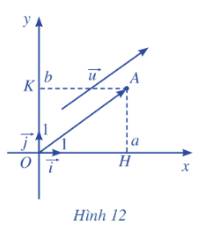
a) Do \(\overrightarrow {OA} {\rm{ }} = {\rm{ }}\overrightarrow u \) nên tọa độ vecto \(\overrightarrow {OA} = \left( {a;b} \right)\). Vậy tọa độ điểm A là: \(A\left( {a;b} \right)\)
b) TỌa độ điểm H là \(H\left( {a;0} \right)\) nên \(\overrightarrow {OH} = \left( {a;0} \right)\). Do đó, \(\overrightarrow {OH} = a\overrightarrow i \)
c) TỌa độ điểm K là \(K\left( {0;b} \right)\) nên \(\overrightarrow {OK} = \left( {0;b} \right)\). Do đó, \(\overrightarrow {OK} = b\overrightarrow j \)
d) Ta có: \({\rm{ }}\overrightarrow u = \overrightarrow {OA} {\rm{ }} = \overrightarrow {OH} + \overrightarrow {OK} = a\overrightarrow i + b\overrightarrow j \) (đpcm)

a) Ta có: \({\overrightarrow i ^2} = {\left| {\overrightarrow i } \right|^2} = 1;{\overrightarrow j ^2} = {\left| {\overrightarrow j } \right|^2};\overrightarrow i .\overrightarrow j = 0\)(vì \(\overrightarrow i \bot \overrightarrow j \) )
b) Ta có: \(\overrightarrow u .\overrightarrow v = \left( {{x_1}\overrightarrow i + {y_1}\overrightarrow j } \right).\left( {{x_2}\overrightarrow i + {y_2}\overrightarrow j } \right) = {x_1}{x_2}.{\overrightarrow i ^2} + {x_1}{y_2}.\left( {\overrightarrow i .\overrightarrow j } \right) + {y_1}{x_2}.\left( {\overrightarrow j .\overrightarrow i } \right) + {y_1}{y_2}.{\overrightarrow j ^2} = {x_1}{x_2} + {y_1}{y_2}\)
AB=( 5;6)