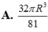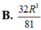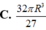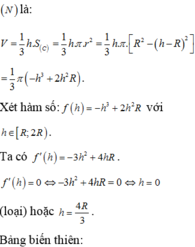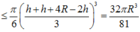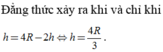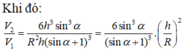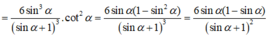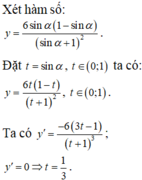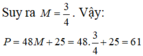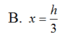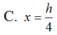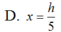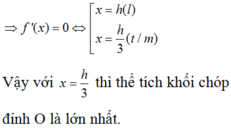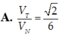Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

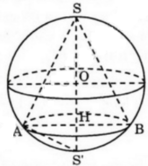
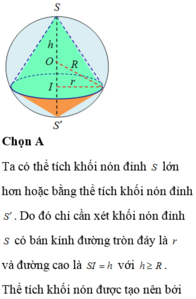
Gọi H là tâm mặt đáy của hình nón, O là tâm mặt cầu (S), đường thẳng IH cắt mặt cầu (S) tại điểm K.


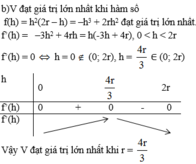
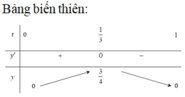
V H ' lớn nhất khi f(r) = r 2 (R - r) (với 0 < r < R) là lớn nhất. Khảo sát hàm số f(r), với 0 < r < R. Ta có f'(r) = 2Rr - 3 r 2 = 0, khi r = 0 (loại), hoặc r = 2R/3. Lập bảng biến thiên ta thấy f(r) đạt cực đại tại r = 2R/3.
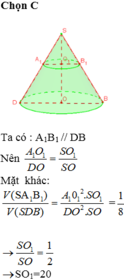
Khi đó ![]()

- Nếu H nằm ở nửa dưới đoạn SO thì \(R\ge\dfrac{SO}{2}=\dfrac{3}{2}\)
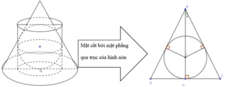
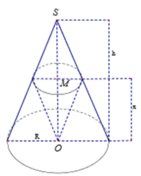
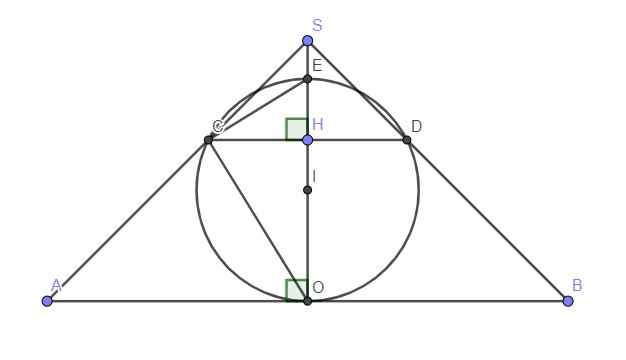
- Nếu H nằm ở nửa trên đoạn SO, thực hiện mặt cắt qua trục nón như hình vẽ
\(SO=OA=3\Rightarrow SOA\) vuông cân \(\Rightarrow SCH\) vuông cân
\(\Rightarrow CH=SH=3-OH=3-\left(R+IH\right)=3-R-\sqrt{R^2-CH^2}\)
\(\Rightarrow3-R=CH+\sqrt{R^2-CH^2}\le\sqrt{2\left(CH^2+R^2-CH^2\right)}=R\sqrt{2}\)
\(\Rightarrow R\left(\sqrt{2}+1\right)\ge3\Rightarrow R\ge\dfrac{3}{\sqrt{2}+1}=3\left(\sqrt{2}-1\right)\)
\(V_{min}=\dfrac{4}{3}\pi R_{min}^3=8,037\)