Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1
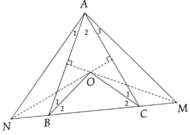
Gọi I là giao điểm của đường thẳng d và AB
Xét tam giác AMN và tam giác BMN có:
Góc MIA = góc MIB = góc AIN = góc NIB (d là đường trung trực của AB)
IA = IB (d là đường trung trực của AB)
=> Tam giác MAN = tam giác MBN (g.c.g)
=> MA = MB; NA = NB (2 cạnh tương ứng)

a) Xét ΔBNP có
BA là đường trung trực ứng với cạnh PN(gt)
nên ΔBNP cân tại B(Định lí tam giác cân)
b) Xét ΔMBN vuông tại M và ΔCBP vuông tại C có
BN=BP(cmt)
\(\widehat{MBN}=\widehat{CBP}\)(hai góc đối đỉnh)
Do đó: ΔMBN=ΔCBP(cạnh huyền-góc nhọn)

a: Xét ΔPAN có
PM là đường trung tuyến
PM là đường cao
DO đó: ΔPAN cân tại P
b: \(MP=\sqrt{5^2-4^2}=3\left(cm\right)\)
Xét ΔPNA có
PM là đường trung tuyến
NB là đường trung tuyến
PM cắt NB tại G
Do đó; G là trọng tâm của ΔPAN
Suy ra: PG=2/3PM=2(cm)


??????????????
Đéo hiể đề bài cho đoạn thẳng phân biệt
mà đòi cm trung trực mới chất
t chịu ok
Vì MA = MB => MN là trung tuyến
mà NB = NA => tam giác ANB cân tại N
=> MN là trung trực
study well